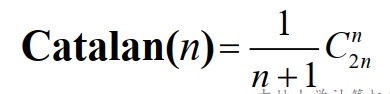二叉树的存储与操作

二叉树的存储结构

  • 顺序存储
    即将左孩子存储在2i,将右孩子存储在2i+1
    比较适合完全二叉树，对于非完全二叉树有空间浪费
  • 链接存储
    二叉链表：left data right
    三叉链表：left data parent right

二叉树的遍历及递归算法

先序遍历

1
2
3
4
5
6
7
void Preorder(TreeNode* t)
{
    if(t==NULL) return;
    visit(t->data);
    Preorder(t->left);
    Preorder(t->right);
}

中序遍历

1
2
3
4
5
6
7
void Inorder(TreeNode* t)
{
    if(t==NULL) return;
    Preorder(t->left);
    visit(t->data);
    Preorder(t->right);
}

后序遍历

1
2
3
4
5
6
7
void Postorder(TreeNode* t)
{
    if(t==NULL) return;
    Preorder(t->left);
    Preorder(t->right);
    visit(t->data);
}

遍历的非递归算法

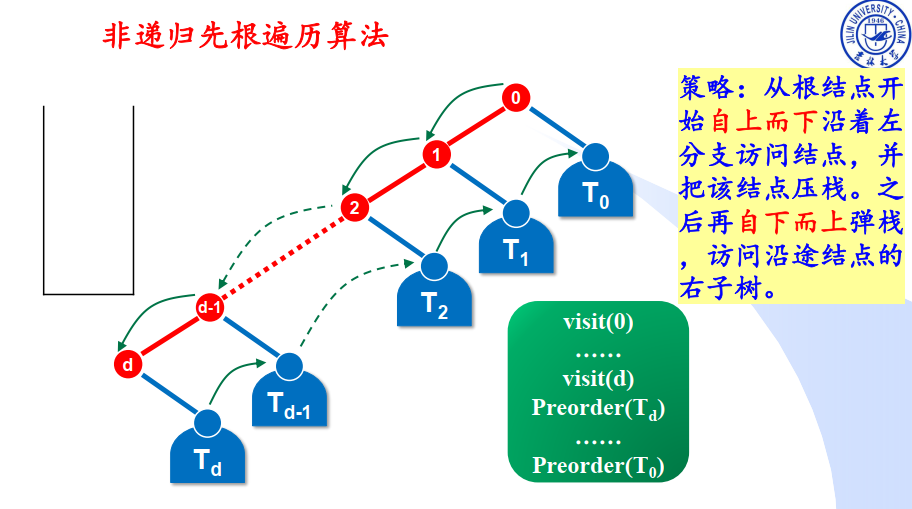
先序遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
void  Preorder(TreeNode* t)
{
    Stack S;
    TreeNode* p=t;
    while(true)
    {
        while(p!=NULL)//自上而下沿左分支访问
        {
            visit(p->data);
            S.push(p);
            p=p->left;
        }
        if(S.empty()) return;//弹栈之前确认栈是否为空
        p=S.pop();//弹栈,自下而上访问各右子树
        p=p->right;
    }
}

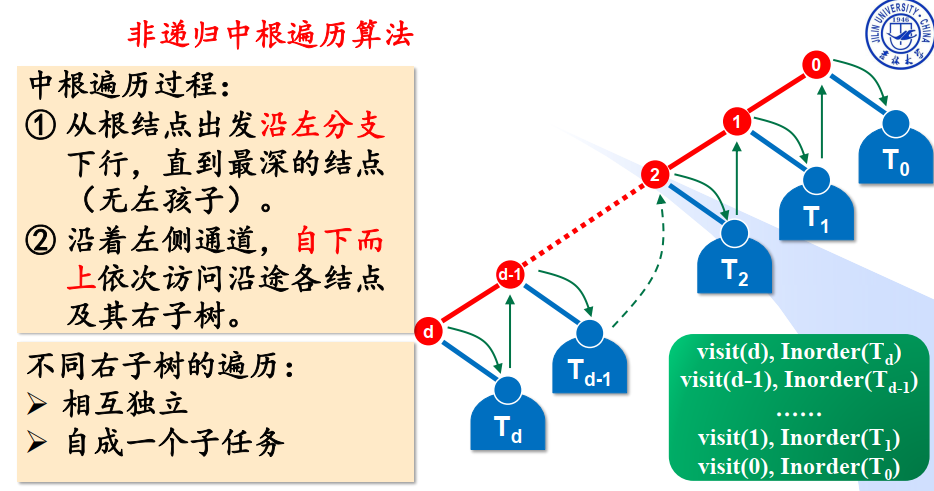
中序遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
void InOrder(TreeNode* t)
{
    Stack S;
    TreeNode p=t;
    while(true)
    {
        while(p!=NULL)//自上而下沿左分支访问
        {
            S.push(p);
            p=p->left;
        }
        if(S.empty()) return;//弹栈之前确认栈是否为空
        p=S.pop();//弹栈,自下而上访问各右子树
        visit(p->data);
        p=p->right;

    }
}

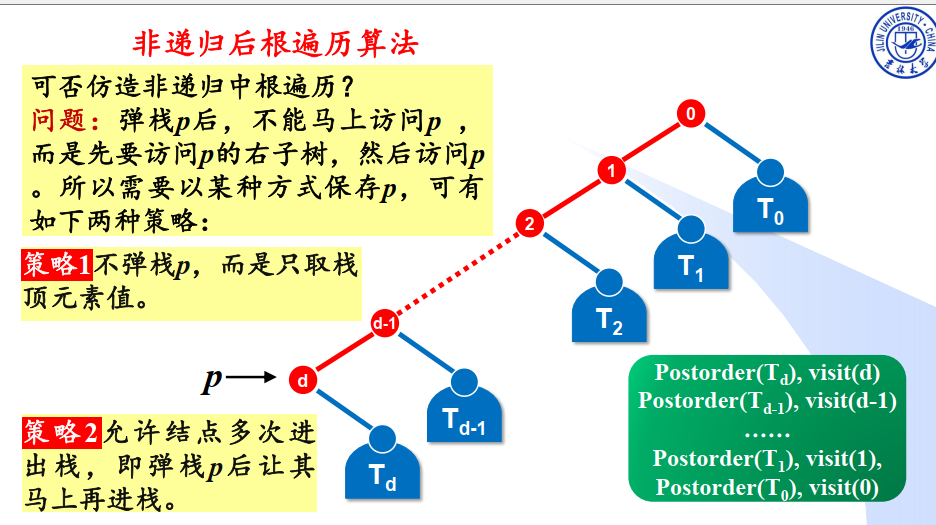
后序遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
void PostOreder(TreeNode* t)
{
    Stack S;
    TreeNode* p=t;
    TreeNode* pre=NULL;//保存上一步访问的结点
    while(true)
    {
        while(p!=NULL)
        {
            S.push(p);
            p=p->left;
        }
        if(S.empty()) return;
        p=S.peak();
        if(p->right==NULL||p->right==pre)//若p无右子树或者p的右子树刚刚访问完，弹出p，访问p
        {
            p=S.pop();
            visit(p->data);
            pre=p;
            p=NULL;
        }
        else
            p=p->right;
    }
}

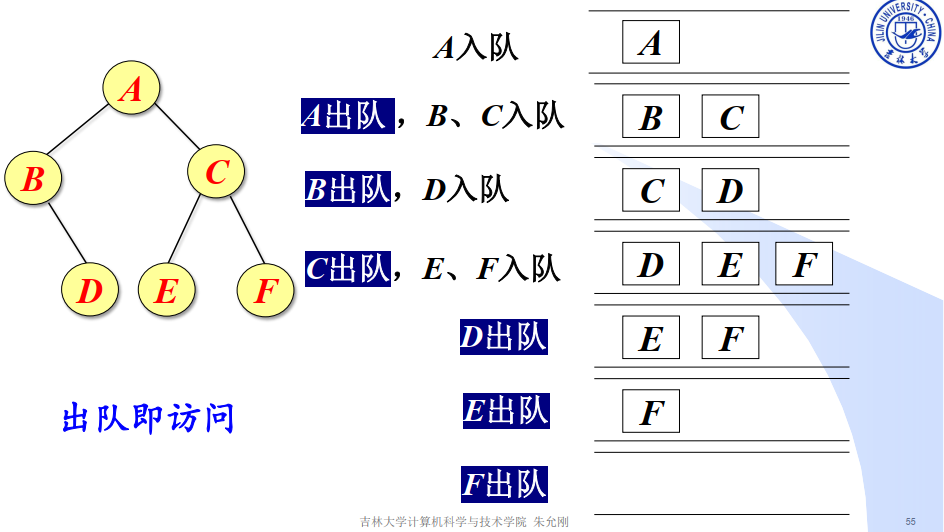
层次遍历

1
2
3
4
5
6
7
8
9
10
11
12
void LevelOrder(TreeNode* t)
{
    Quene Q;
    if(t!=NULL) Q.enquene(t);
    while(!Q.empty())
    {
        TreeNode* p=Q.dequeue();
        visit(p->data);
        if(p->left) Q.enqueue(p->left);
        if(p->right) Q.enqueue(p->right);
    }
}

辅助队列的规模
最大规模：n/2（向上取整）

统计每层结点信息

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
int LeafInEachLevel(TreeNode* root,int leafnum[])//leafnum记录每层叶节点数量
{
    if(root==NULL) return -1;
    Queue q;
    int level=0;
    q.enqueue(root);
    while(!q.empty())
    {
        int size=q.size();
        for(int i=0;i<size;i++)
        {
            TreeNode* p=q.dequeue();
            if(p->left==NULL&&p->right==NULL) leafnum[level]++;
            if(p->left) q.enqueue(p->left);
            if(p->right) q.enqueue(p->right);
        }
        level++;
    }
    return level-1;
}

二叉树的重建与计数

二叉树的重建

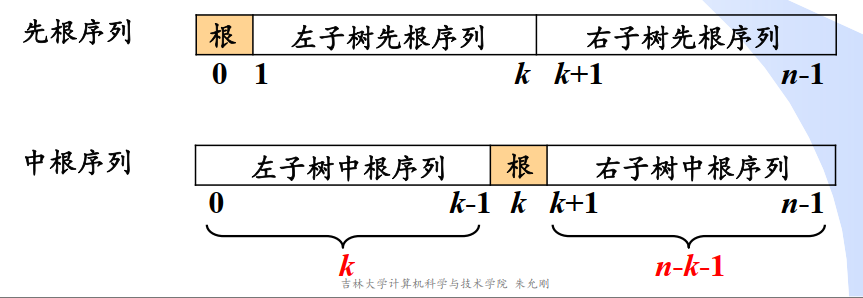
中根序列和任意一种遍历序列都可以唯一确定一棵二叉树
给定二叉树的先根序列和中根序列， 编写程序构建二叉树。
【 大 厂 面 试 题 、 华 中 科 技 大 学 考 研 复 试 机 试 题 、
OpenJudgeP0570、 LeetCode105】

1
2
3
4
5
6
7
8
9
10
11
TreeNode* buildtree(char* preorder,char* inorder,int n)
{
    if(n<=0) return NULL;
    char rootval=preorder[0];//先序序列根的val
    TreeNode* root=new TreeNode;
    root->val=rootval;
    int k=find(inorder,n,rootval);//在中序序列里找根，根左边即左子树的中序，右边即右子树的中序
    root->left=buildtree(&preorder[1],&inorder[0],k);
    root->right=buildtree(&preorder[k+1],&inorder[k+1],n-k-1);
    return root;
}

二叉树的计数

Cantalan(n)

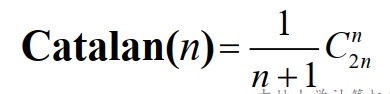
二叉树的其他操作

解决二叉树问题的一般框架

算法 f(root)
{
可在此处处理根节点
f(root->left);
可在此处处理根节点
f(root->right)
可在此处处理根节点
return;
}

如，在二叉树中搜索给定结点的父结点

1
2
3
4
5
6
7
8
9
TreeNode* Father(TreeNode* root,TreeNode* p)
{
    if(root==NULL||p==root) return NULL;
    if(root->left==p||root->right==p) return root;//根结点为父节点（中）
    TreeNode* fa=Father(root->left,p);//左
    if(fa!=NULL) return fa;
    return Father(root->right,p);//右

}

创建二叉树

通过一种遍历序列不能唯一确定二叉树，因为在二叉树中，有的节点之左/右指针为空，这在先根序列中不能被体现。
增强先根序列：空指针处用#表示

  • 根据增强先根序列创建二叉树

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    char s[N];
    int k=0;
    TreeNode* CreateBinTree(char preorder[])
    {
        char ch=preorder[k++];
        if(ch=='#') return NULL;
        TreeNode* t=new TreeNode;
        t->data=ch;//中
        t->left=CreateBinTree(preorder);//左
        t->right=CreateBinTree(preorder);//右
        return t;
    }
    int main()
    {
        scanf("%s",s);
        TreeNode* root=CreateBinTree(s);
    }

  • 上机实验常用创建形式

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    TreeNode* CreateBinTree()
    {
        int k;
        cin>>k
        if(k==0) return NULL;
        TreeNode* t=new TreeNode;//中
        t->data=k;
        t->left=CreateBinTree();//左
        t->right=CreateBinTree();//右
        return t;
    }

二叉树中、先、后根序列的首末结点


中根序列
第一个结点，向左走到头
最后一个结点，同理，向右走到头
先根序列
第一个结点，root
最后一个节点：从根节点开始沿右分支找第一个叶结点，若找不到则在最右边结点的左子树沿右分支找叶结点
后根序列
第一个结点：从根节点开始沿左分支找第一个叶结点，若找不到则在最左边结点的右子树沿左分支找叶结点
最后一个节点：root

二叉树的路径

输出从根到叶的所有路径，k为递归深度

1
2
3
4
5
6
7
8
9
10
11
12
13
14
void findpath(TreeNode* t,int path[],int k)
{
    if(t==NULL) return;
    path[k]=t->data;
    if(t->left==NULL&&t->right==NULL)//中，t到叶子结点，找到一条路径
    {
        for(int i=0;i<k;i++)
            printf("%d ",path[i]);
        printf("\n");
        return;
    }
    findpath(t->left,path,k+1);//左
    findpath(t->right,path,k+1);//右
}

输出从根到数据值为x的一条路径，k为递归深度

1
2
3
4
5
6
7
8
9
10
11
12
13
void FindPath(TreeNode* t,vector<int>path,int k,int x,vector<int>&path)
{
    if(t==NULL) return;
    path.push_back(t->val);
    if(t->val==x)
    {
        for(int i=0;i<=k;i++)
            path.push_back(path[i]);
        return;
    }
    FindPath(t->left,path,k+1,x,path);
    FindPath(t->right,path,k+1,x,path); 
}

二叉树的公共祖先

1
2
3
4
5
6
7
8
9
10
11
12
TreeNode* Traversal(TreeNode*root,int a,int b)
{
    if(root==NULL) return NULL;
    if(root->val==a||root->val==b)
        return root;
    TreeNode* left=Traversal(root->left,a,b);
    TreeNode* right=Traversal(root->right,a,b);
    if(left!=NULL&&right!=NULL) return root;
    else if(left!=NULL&&right==NULL) return left;
    else if(left==NULL&&right!=NULL) return right;
    else return NULL;
}