树和二叉树的应用

压缩与哈夫曼树

最优编码问题
设组成文件的字符集A={a1,a2,…an}，其中ai出现的次数为ci，ai的编码成都为li，设计编码方案使min$\sum_{i=1}^{n}ci*li$

扩充二叉树

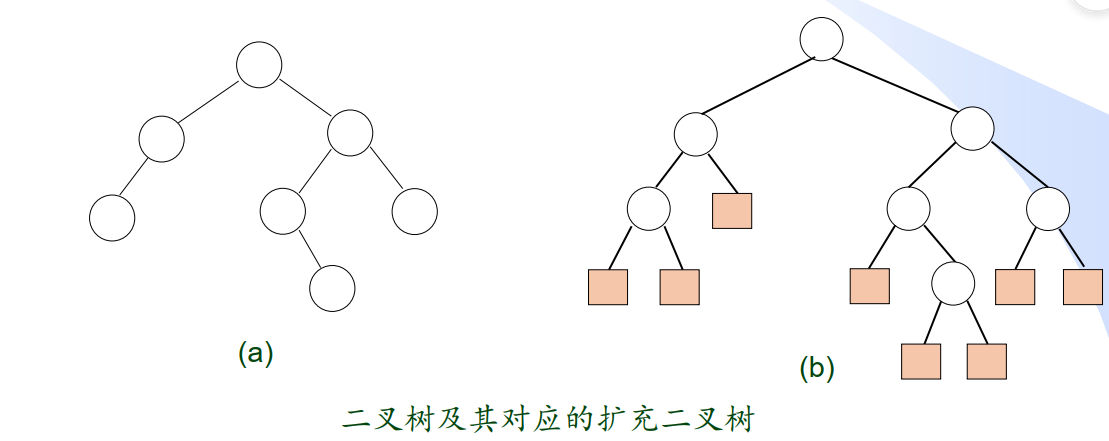
加权路径长度
外结点权值为wi，深度为Li
$WPL=\sum wi*Li$

一种文件编码方案可以映射为一颗扩充二叉树
字符 ==> 外结点
字符出现次数ci ==> 外结点权值wi
字符的编码长度li ==> 外结点深度Li
文件总编码长度 ==> 扩展二叉树WPL值

哈夫曼算法

自下而上
重复做：选择权值最小的两个结点来生成新结点，新结点作为原结点的父亲，权值是原来两个结点权值之和
编码：每个左分支标记为0，右分支标记为1

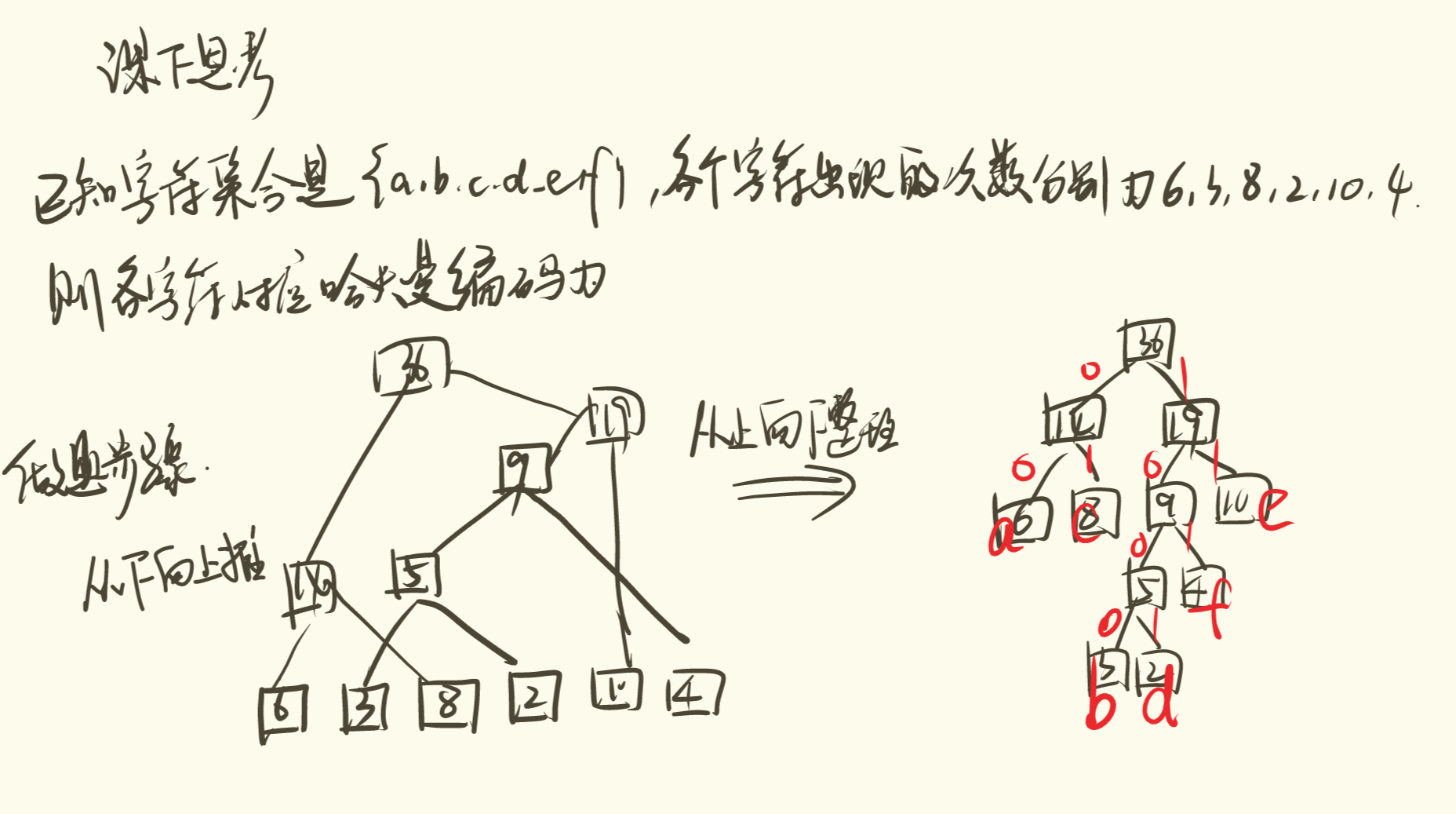
哈夫曼树
二子性 ==> n个叶结点，n-1个非叶结点，2n-1个总结点
同权不同构 ==> 哈夫曼树形态不唯一，编码不唯一，WPL唯一，最小编码长度唯一

哈夫曼算法实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
struct HuffmanNode
{
    char data;
    int weight;
    HuffmanNode* left,*right;
}
const int N=300;
HuffmanNode* H[N];
void CreateHuffmanNode(char ch[],int freq[],int n)//有n种字符，第i种字符放在ch[i],其频率放在freq[i]中
{
    for(int i=0;i<n;i++)
    {
        H[i]=new HaffmanNode;
        H[i]->data=ch[i];
        H[i]->weight=freq[i];
        H[i]->left=H[i]->right=NULL;
    }
    sort(H,n);//对H按weight值递增排序
}
HuffmanNode* CreateHuffmanTree(HuffmanNode* H[],int n)
{
    //int WPL=0;
    for(int i=0;i<n-1;i++)
    {
        HuffmanNode* t=new HuffmanNode;
        t->weight=H[i]->weight+H[i+1]->weight;
        //WPL+=t->weight;
        t->left=H[i]; t->right=H[i+1]; t->data='';
        //把新结点t插入数组中
        int j=i+2;
        while( j<n && H[j]->weight < t->weight)
        {
            H[j-1]=H[j];
            j++;
        }
        H[j-1]=t;
    }
    return H[n-1];
}

哈夫曼树的遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
void traversal(HuffmanNode* t,vector<int>&path)
{
    if(t->left==NULL&&t->right==NULL)//中
    {
        int n=path.size();
        Cnt+=n*t->weight;
        for(int i=0;i<n;i++)
        {
            Path[(int)t->data][i]=path[i];
        }
        Num[(int)t->data]=n;
        return;
    }
    if(t->left)
    {
        path.push_back(0);
        traversal(t->left,path);
        path.pop_back();
    }
    if(t->right)
    {
        path.push_back(1);
        traversal(t->right,path);
        path.pop_back();
    }
}

译码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
void decode(HuffmanNode* t,vector<int>code)
{
    vector<char>path;
    int n=code.size();
    int i=0;
    HuffmanNode* origin=t;
    while(i<n)
    {
        while(t->left!=NULL||t->right!=NULL)
        {
            if(t==NULL||i>=n)
            {
                cout<<"INVALID"<<endl;
                return;
            }
            if(code[i]==0)
                t=t->left;
            else
                t=t->right;
            i++;
        }
        path.push_back(t->data);
        t=origin;
    }
    for(int i=0;i<(int)path.size();i++)
        cout<<path[i];
    cout<<endl;
    
}

不建树求WPL【北京邮电大学机试】

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
int CreateHuffmanTree(int weight[],int n)
{
    sort(weight,n);//对weight数组递增排序,需要预先实现
    int WPL=0;
    for(int i=0;i<n-1;i++)
    {
        int t=weight[i]+weight[i+1];
        WPL+=t;
        int j=i+2;
        while(j<n && t>weight[i])//向右移，故要找到第一个大于他的数
            weight[j-1]=weight[j];
        weight[j-1]=t;
    }
    return WPL;
}

给定树，求WPL

1
2
3
4
5
6
7
8
9
int WPL=0;
void WPLPreOrder(TreeNode* t,int k)//k为递归深度
{
    if(t==NULL) return;
    if(t->left==NULL && t->right==NULL)
        WPL+=t->weight * k;
    WPLPreOrder(t->left,k+1);
    WPLPreOrder(t->right,k+1);
}

表达式树

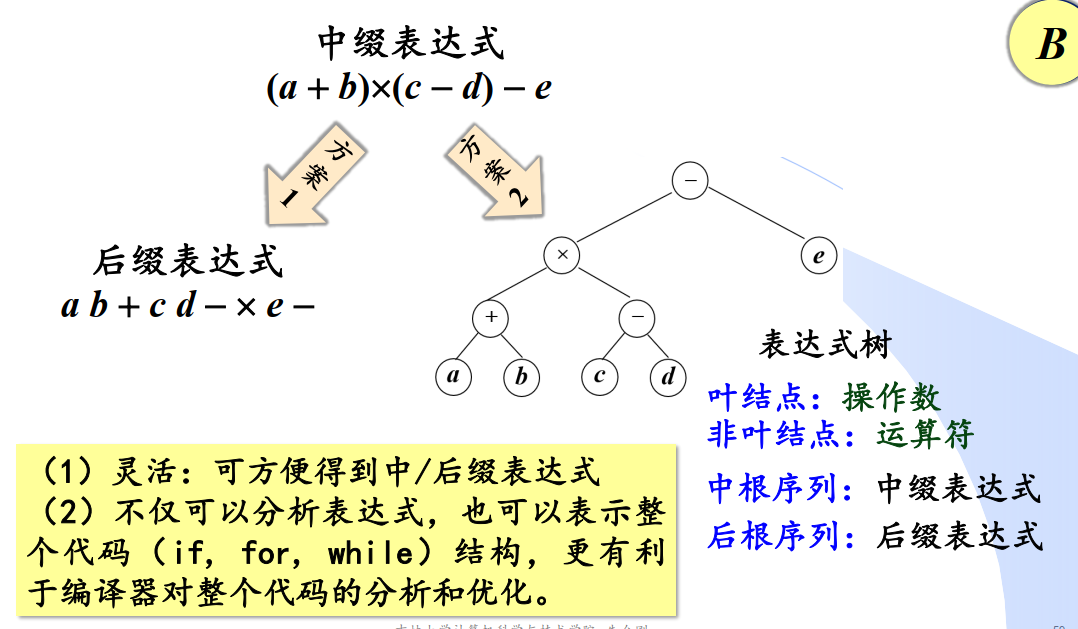
根据后缀表达式构造表达式二叉树

从左到右扫描后缀表达式，扫描到一个符号就生成一个结点，符号位结点数据域值

  • 操作数：将操作数结点压栈
  • 运算符：从栈中弹出两个结点，分别作为当前运算符的左右孩子，再将当前运算符结点压栈
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    TreeNode* buildExpTree(char* s,int n)
    {
        stack<TreeNode*>S;
        for(int i=0;i<n;i++)
        {
            TreeNode* p=new TreeNode;
            p->data=s[i];
            if(s[i]>='a' && s[i] <='z')
                p->left=p->right=NULL;
            else
            {
                p->right=S.pop();
                p->left=S.pop();
            }
            S.push(p);
        }
        return S.peak();
    }

计算表达式二叉树对应的值

1
2
3
4
5
6
7
8
9
10
11
12
int Calc(TreeNode* t)
{
    if(t->left==NULL && t->right==NULL)//操作数
        return t->data-'0';
        int ans1=Calc(t->left);
        int ans2=Calc(t->right);
        char op=t->data;
        if(op=='+') return ans1+ans2;
        else if(op=='-') return ans1-ans2;
        else if(op=='*') return ans1*ans2;
        else return ans1/ans2;
}

并查集

并查集的实现

  • MAKE_SET(x):为x生成一颗单结点树，x为根节点
  • UNION(x,y)：合并x所在的树和y在的树，让其中一棵树的根的复制真只想另一棵树的根。
  • FIND(x)：查找x所在树的根结点

用Father数组表示集合

1
2
3
4
5
6
7
8
9
10
11
12
13
void MS(int x)
{
    Father[x]=0;
}
int FD(int x)
{
    if(Father[x]==0) return x;
    return FD(Father(x));
}
void UN(int x,int y)
{
    Father[FD(y)]==FD(x);
}

并查集的优化

  • 路径压缩
    在FIND(x)的操作中，找到元素x所在树的根fx之后，将x到fx路径上所有结点的父亲都改成fx
    1
    2
    3
    4
    5
    6
    int FIND(int x)
    {
        if(Father[x]==0) return x;
        Father[x]=FIND(Father[x]);
        return Father[x];
    }
  • 按秩合并
    每个结点维护一个秩，表示以该节点为根的子树的高度的上界
    合并：秩大的根做秩小的根的父亲
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    void UNION(int x,int y)
    {
        int fx=FIND(x);
        int fy=FIND(y);
        if(fx==fy) return;
        if(rank[fx]>rank(fy))
        Father[fy]=fx;
        else
        {
            Father[fx]=fy;
            if(rank[fx]==rank[fy])
            rank[fy]++;
        }
    }
    如果x是根结点，Father[x]存秩的相反数
    否则，Father[x]存x的父亲地址

最终版本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
void Make_Set(int x)
{
    Father[x]=0;
}
int FIND(int x)
{
    if(Father[x]<=0) return x;//x是根
    Father[x]=Find(Father[x]);
    return Father[x];
}
void UNION(int x,int y)
{
    int fx=Find(x); int fy=FIND(y);
    if(fx==fy) return;
    if(Father[fx]<Father[fy])//存的相反数，实际大于
        Father[fy]=fx;
    else
    {
        Father[fx]==fy;
        if(Father[fx]==Father[fy])
            Father[fy]--;//fy秩+1
    }
}

并查集的应用–等价性问题

自反，对称，传递