拓扑排序和关键路径

拓扑排序

一个任务通常可以被分解成若干个子任务，某些情况下，子任务要求有序

基本概念

AOV网

  • 在有向图中，顶点表示活动，有向边表示活动间的先后关系，称这样的有向图为AOV网
  • 在AOV网中，如果活动Vi必须在活动Vj之前进行，则存在有向边Vi->Vj
  • AOV网中不能出现有向回路，即有向环，否则意味着某项活动以自己为先决条件

拓扑序列：把AOV网中的所有顶点排成一个线性序列，在拓扑序列中，先进性的任务一定在后进行的任务前面，按照拓扑序列完成各子任务，就可以顺利完成整个任务
拓扑排序：构造AOV网的拓扑序列的过程

拓扑排序算法的基本步骤

  1. 从图中选择一个入度为0的顶点并输出
  2. 从图中删除该顶点及该顶点引出的所有边
  3. 执行①②，直至所有顶点已输出，或图中剩余顶点入度均不为0（说明存在环）
    对于任何无环的AOV网，其顶点均可排成拓扑序列，其拓扑序列未必唯一

拓扑排序的实现

准备工作（假定AOV网以邻接表的形式存储）

  • 数组InDegree[]:InDegree[i]作为顶点i的入度
  • 建立一个栈存放入度为0的顶点，每当一个顶点呃入度为0，就将其压栈，每次找入度为0的顶点时，就弹栈

求每个顶点的入度

1
2
3
4
5
6
7
8
9
10
11
12
13
14
void getIndegree(Vertex Head[],int n,int InDegree[])
{
    for(int i=0;i<n;i++) InDegree[i]=0;
    for(int i=0;i<n;i++) //扫描顶点
    {
        Edge* p=Head[i].adjacent;
        while(p!=NULL) //扫描边
        {
            int k=p->VerAdj;
            InDegree[k]++;
            p=p->link;
        }
    }
}
1
2
3
4
5
6
7
8
9
10
11
void getInDree(Vertex Head[],int n,int InDegree[])
{
    for(int i=0;i<n;i++) InDegree[i]=0;
    for(int i=0;i<n;i++) //扫描顶点
    {
        for(Edge* p=Head[i]->adjacent;p!=NULL;p=p->link)
        {
            InDegree[p->VerAdj]++;
        }
    }
}

拓扑排序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
bool TopoOrder(Vertex Head[],int n)
{
    int InDegree[N];
    Stack s;

    getInDegree(Head,n,InDegree);
    for(int i=0;i<n;i++)//入度为0的顶点进栈
        if(InDegree[i]==0)
            s.push(i);

    for(int i=0;i<n;i++)//输出n个顶点
    {
        if(s.empty()) return false;//尚未输出n个顶点就没有入度为0的顶点了，说明有环
        int j=s.pop();
        cout<<j<<" ";
        for(Edge* p=Head[j].adjacent;p!=NULL;p=p->link)
        //删除j和j引出的边，其效果是j的邻接顶点入度减1
        {
            int k=p->VerAdj;
            InDegree[k]--;
            if(InDegree[k]==0) s.push(k);
        }
    }
    return true;
}

判断拓扑序列

关键路径

AOV网：顶点表示活动或任务，有向边表示活动（或任务）间的相互关系
AOE网：有向边表示活动或任务，用边上的权值表示活动的持续时间，顶点称为事件，表示其入边的任务已完成，出边的任务可开始的状态
关键路径：完成整个工程所需的最短时间取决于从源点到汇点的最长路径长度，这条路径最长的路径就叫做关键路径
关键活动：关键路径上的活动

与关键活动有关的量

事件Vj的最早发生时间：ve(j) 最晚发生时间vl(j)
活动ai的最早发生时间：e(i) 最晚发生时间l(i)

  1. 事件Vj的最早发生时间ve(j)
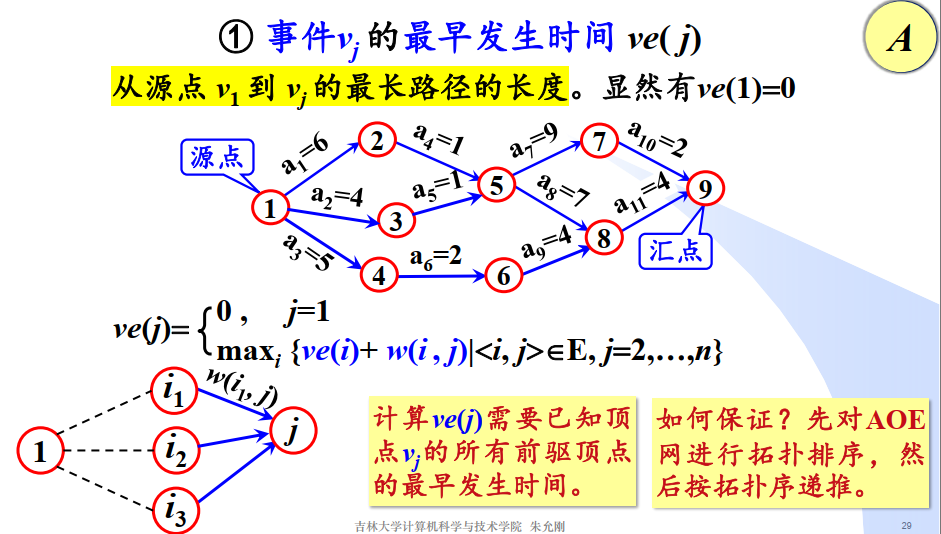
  2. 事件Vj的最迟发生时间vl(j)
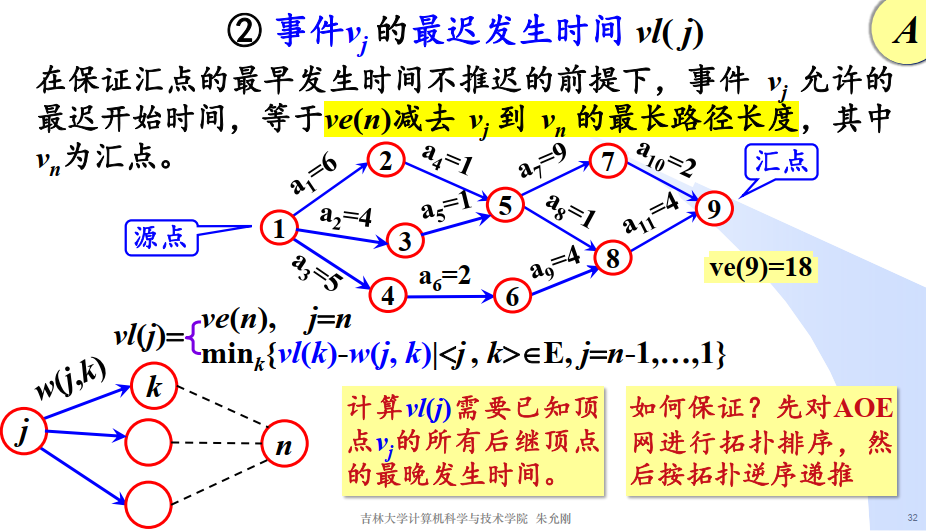
  3. 活动ai的最早开始时间e(i)
  4. 活动ai的最迟开始时间l(i)

关键路径和关键活动

关键路径：从源点到汇点的最长路径
关键活动：关键路径上的或从，活动的最早开始时间等于活动的最迟开始时间，即l(i)=e(i)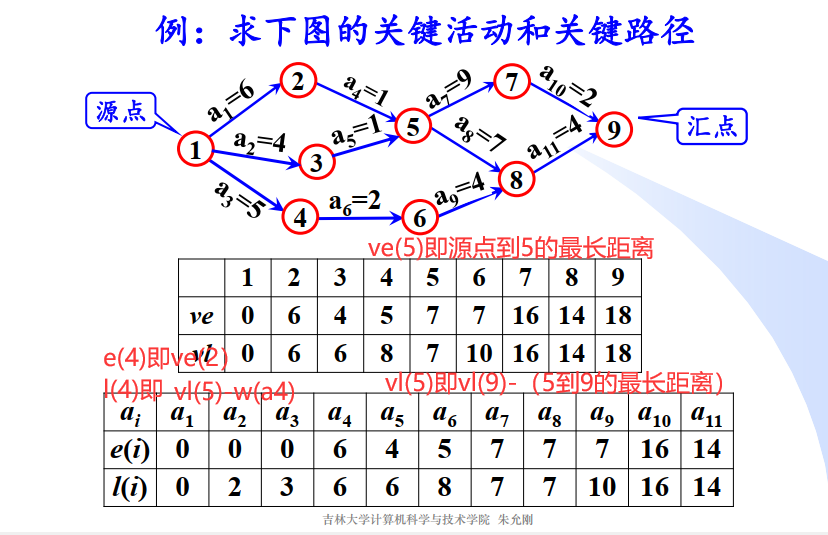

计算ve

计算顶点的最早发生时间，存入ve数组（假定图中顶点已按拓扑序编号）

1
2
3
4
5
6
7
8
9
10
11
12
13
void VertexEarliestTime(Vertex Head[],int n,int ve[])
{
    for(int i=1;i<=n;i++)
        ve[i]=0;

    for(int i=1;i<=n;i++)
        for(Edge* p=Head[i].adjacent;p!=NULL;p=p->link)
        {
            int k=p->veradj;
            if(ve[i]+p->cost>ve[k])
                ve[k]=ve[i]+p->cost;
        }
}

图中顶点未按拓扑序编号

  1. 方案一：先执行拓扑排序，将拓扑序存在数组Topo
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    void VertexEarliestTime(Vertex Head[],int Topo[],int n,int ve[])
    {
        //拓扑序存储在Topo数组中
        for(int i=1;i<=n;i++)
            ve[i]=0;

        for(int i=1;i<=n;i++)
            for(Edge* p=Head[Topo[i]].adjacent;p!=NULL;p=p->link)
            {
                int k=p->veradj;
                if(ve[Topo[i]]+p->cost>ve[k])
                    ve[k]=ve[Topo[i]]+p->cost;
            }
    }
  2. 拓扑排序过程中顺带更新ve，无需调用上述函数
    原理
    拓扑排序：按拓扑序选出一个点，扫描其邻接顶点k，更新顶点k的入度
    求ve值：按拓扑序选出一个点，扫描其邻接顶点k，更新顶点k的ve值
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    void TopoOrder(Vertex Head[],int n)
    {
        int InDegree[N];
        Stack s;
        InDegree(Head,n,InDegree);//求每个点的入度

        for(int i=1;i<=n;i++)
            if(InDegree[i]==0)
                s.push(i);
        
        for(int i=1;i<=n;i++)
        {
            if(s.empty()) return;//有环
            int j=s.pop();//选出入度为0的点
            for(Edge* p=Head[j].adjacent;p!=NULL;p=p->link)
            {
                int k=p->veradj;
                InDegree[k]--;
                if(InDegree[k]==0) s.push(k);
            }
            if(ve[j]+p->cost>ve[k]) ve[k]=ve[j]+p->cost;
        }
    }

计算vl

1
2
3
4
5
6
7
8
9
10
11
12
13
void VertexLatestTime(Vertex Head[],int n,int ve[],int vl[])
{
    for(int ni=1;i<=n;i++)
        vl[i]=ve[n];
    
    for(int i=n;i>=1;i--)
        for(Edge* p=Head[i].adjacent;p!=NULL;p=p->link)
        {
            int k=p->veradj;
            if(vl[k]-p->cost < vl[i])
                vl[i]=vl[k]-p->cost;
        }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
void VertexLatestTime(Vertex Head[],int n,int Topo[],int ve[],int vl[])
{
    for(itn i=1;i<=n;i++)
        vl[i]=ve[Topo[n]];//不是处理顶点i,而是拓扑序的第i的顶点

    for(int i=n;i>=1;i--)
        for(Edge* p=Head[Topo[i]].adjacent;p!=NULL;p=p->link)
        {
            int k=p->veradj;
            if(vl[k]-p->cost < cl[Topo[i]])
                vl[Topo[i]]=vl[k]-p->cost;
        }
}

计算活动的最早和最迟开始时间

1
2
3
4
5
6
7
8
9
10
11
void ActivityStartTime(Vertex Head[],itn n,int ve[],int vl[])
{
    for(int i=1;i<=n;i++)
        for(Edge* p=Head[i].adjacent;p!=NULL;p=p->link)
        {
            int k=p->veradj;
            int e=ve[i];//i是线段左端点
            int l=vl[k]-p->cost;//k是线段右端点
            if(e==l) printf("%d->%d\n",i,k);//输出关键活动
        }
}