图的最短路径
无权图最短路径 BFS
无权图的单源最短路径问题
准备工作
dist[]:从源点到顶点i的最短距离,即Di,初值∞
pre[]:从源点到顶点i的最短路径中顶点i的前驱顶点,初值-1
∞的表示:INT_MAX / 0x3f3f3f3f
const int INF=ox3f3f3f3f;
基于BFS的无权图最短路径算法
时间复杂度O(n+e)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
| const int INF=ox3f3f3f3f;
void BFS(Vertex Head[],int n,int u,int dist[],int pre[])
{
Queue Q;
for(int i=1;i<=n;i++)
{
pre[i]=-1;
dist[i]=INF;
}
dist[u]=0;
Q.enqueue(u);
while(!Q.empty())
{
int v=Q.dequeue();
for(Edge* p=Head[i].adjacent;p!=NULL;p=p->link)
{
int w=p->veradj;
if(dist[w]==INF)
{
dist[w]=dist[v]+1;
pre[w]=v;
Q.enqueue(w);
}
}
}
}
|
Dijkstra算法
正权图的单元最短路径问题
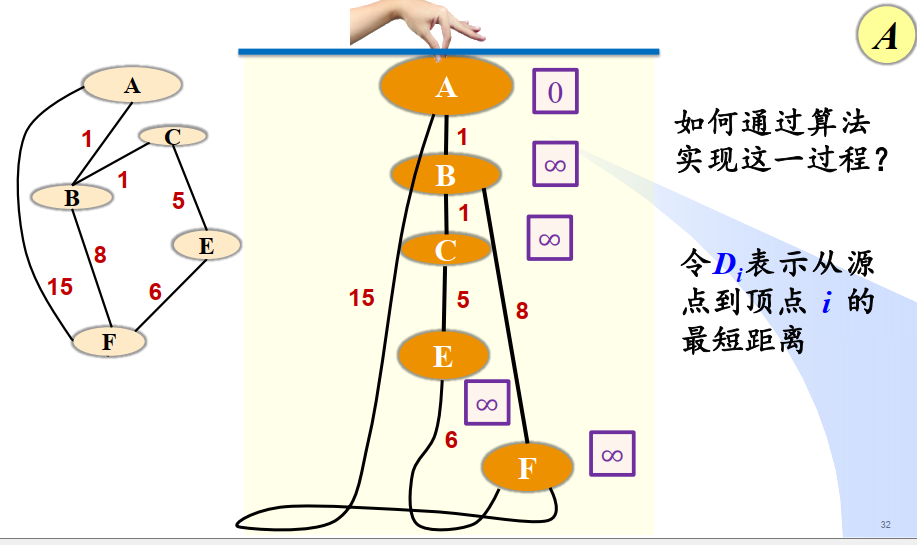
准备三个辅助数组
dist[]:源点u到i的最短距离,初始值∞
pre[]:u到i最短路径上i的前驱顶点编号,初始值-1 【可存源点到所有点的最短路】
S[i]:顶点i是否在集合S中,初始时S[i]=0
时间复杂度O(n^2+e)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
| int findMin(int S[],int dist[],int n)
{
int v=-1,min=INF;
for(int i=1;i<=n;i++)
if(S[i]==0&&dist[i]<min)
{
min=dist[i]
v=i;
}
return v;
}
void Dijkstra(Vertex Head[],int n,int u,int dist[],int pre[])
{
int S[N]={0};
for(int i=1;i<=n;i++)
{
pre[i]=-1;
dist[i]=INF;
}
dist[u]=0;
for(int i=1;i<=n;i++)
{
int v=findMin(S,dist,n);
if(v==-1) return;
S[v]=1;
for(Edge* p=Head[v].adjacent;p!=NULL;p=p->link)
{
int w=p->veradj;
if(S[w]==0 && dist[v]+p->cost < dist[w])
{
dist[w]=dist[v]+p->cost;
pre[w]=v;
}
}
}
}
|
A*算法初探
正权图的单源单目标最短路径问题

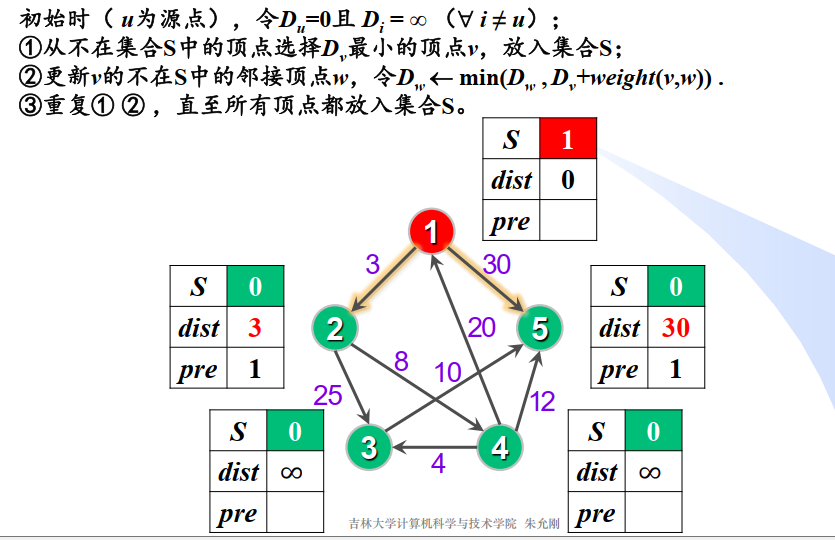
Floyd算法
任意两点间的最短路径问题
Dk是Vi经过顶点集合Ik={v1v2,v3…vk}中的点到达vj的最短路径长度
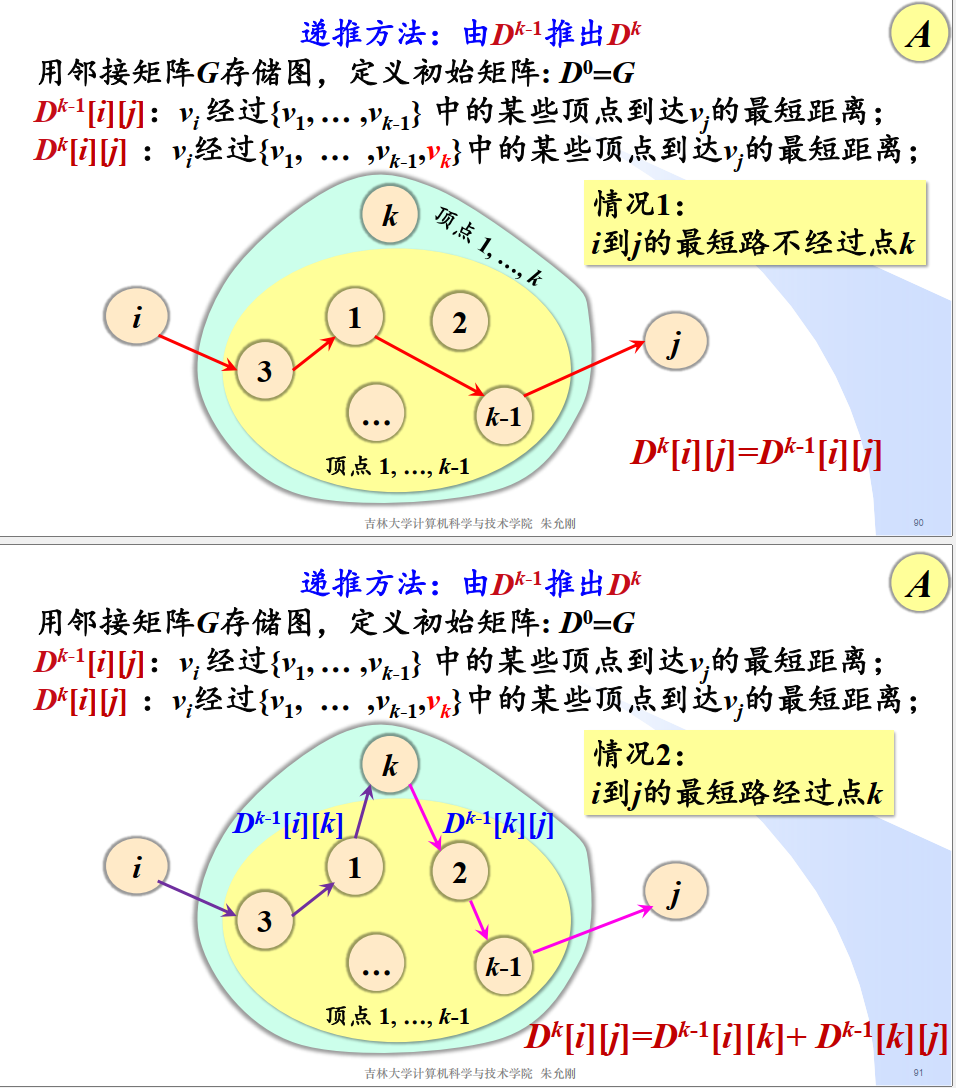
D[i][j]=min{D[i][j],D[i][k]+D[k][j]};
准备工作
D[i][j]:从顶点i到顶点j的最短路径,初值为邻接矩阵
path[i][j]:i到j最短路径上i的下一个顶点的编号
时间复杂度:O(n^3)
不允许存在负环,Floyd算法可以判断负环,若算法执行过程中D[i][i]<0,即存在负环
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
| void Floyd(int G[N][N],int n,int D[N][N],int path[N][N])
{
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
{
D[i][j]=G[i][j];
if(i!=j && G[i][j]<INF)
path[i][j]=j;
else
path[i][j]=-1;
}
for(int k=1;k<=n;k++)
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
{
if(D[i][k]+D[k][j]<D[i][j])
{
D[i][j]=D[i][k]+D[k][j];
path[i][j]=path[i][k];
}
}
}
|
有向图的传递闭包问题
不关注路径长度,而仅关注是否存在路径
可及矩阵:n阶方阵,若顶点vi到vj可及,R[i][j]=1,否则为0
传递闭包:由有向图G的顶点集V,边集E,以及新添加的虚边(表示两点可及)构成的图
R[i][j]=R[i][j] OR (R[i][k] AND R[k][j])
时间复杂度O(n^3)
Warshall算法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
| void Warshall(int G[N][N],int n,int R[N][N])
{
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
{
R[i][j]=G[i][j];
}
for(int k=1;k<=n;k++)
for(int i=1;i<=n;i++)
for(int j=1;j<=1;j++)
R[i][j]=R[i][j]||(R[i][k]&&R[k][j]);
}
|
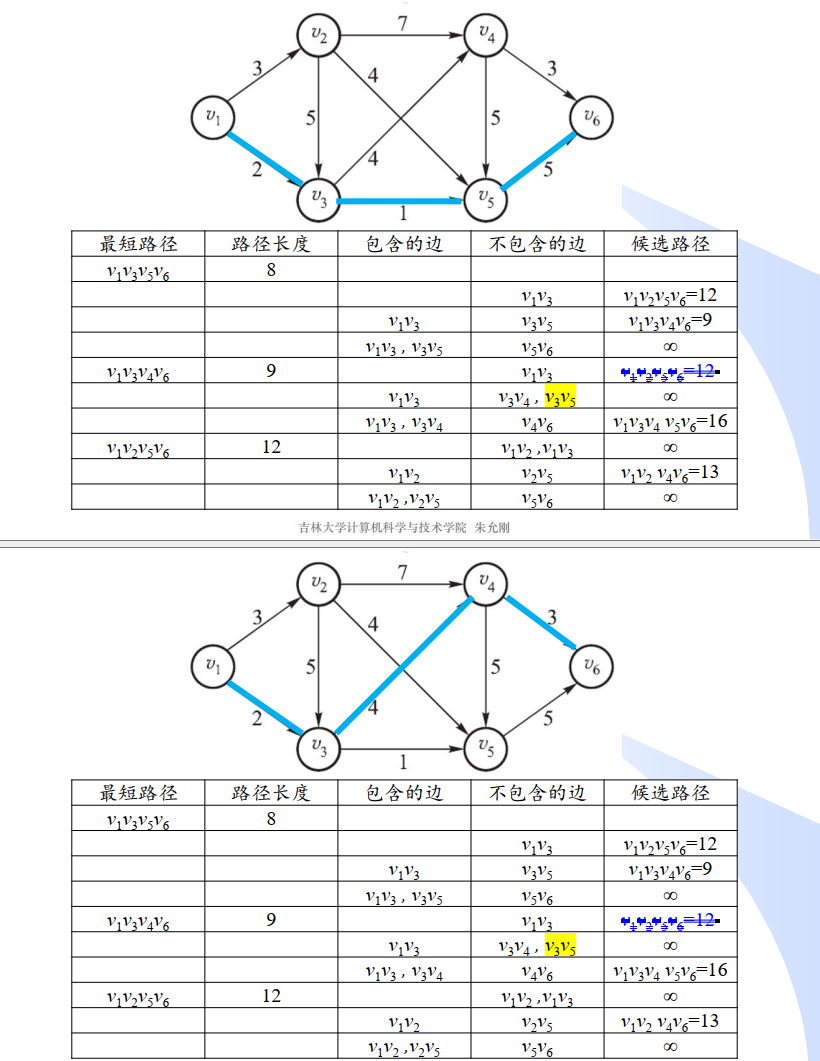
满足约束的最短路径 Yen算法
第k短路径问题
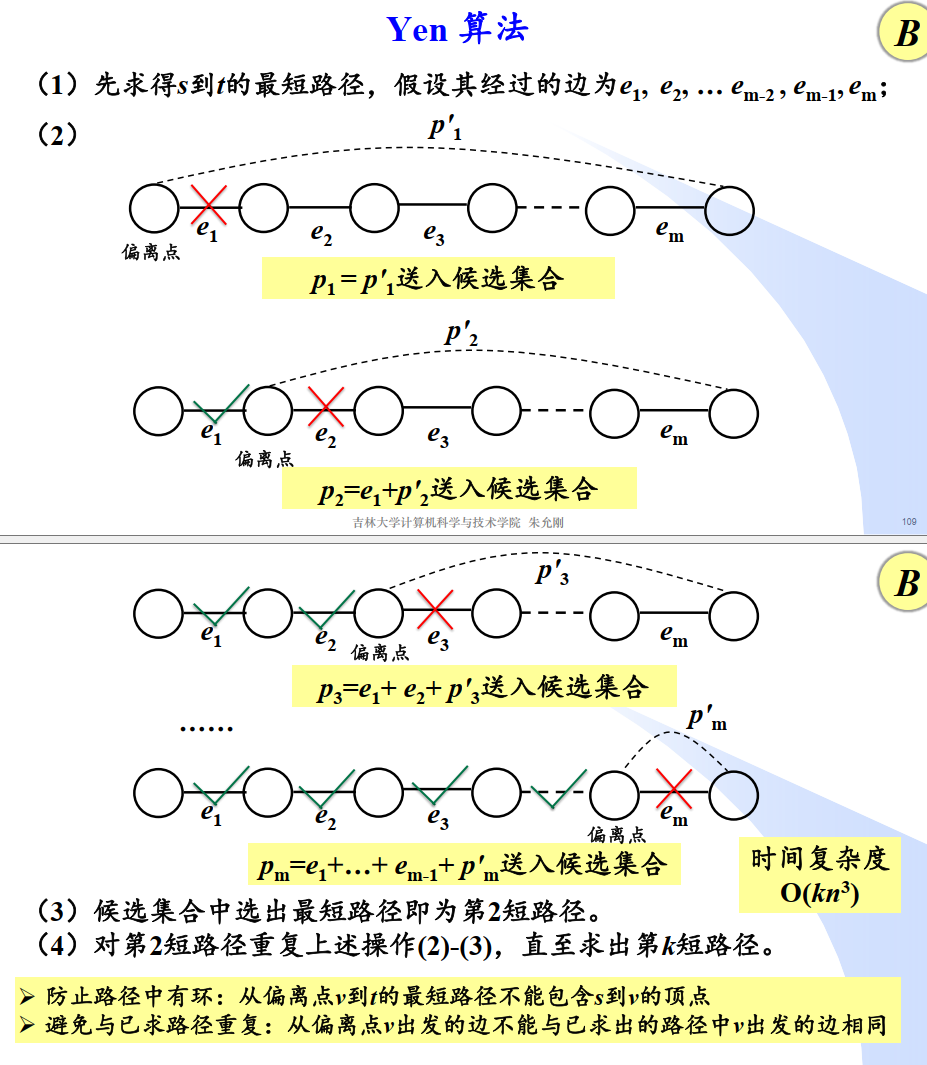
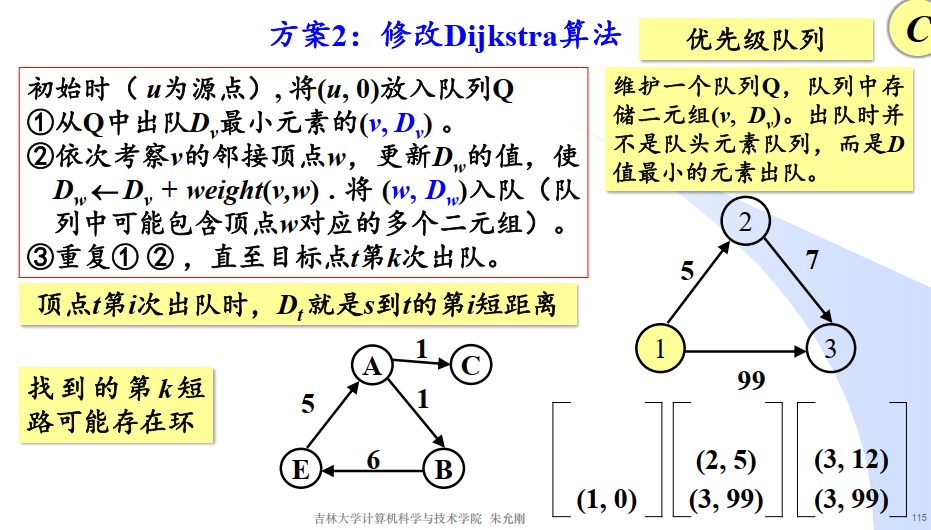
方案2:修改Dijkstra算法
满足约束的最短路径
- 一次生成两个顶点间的第1,2…k短路径
- 然后注意测试每条路径是否满足给定的约束条件
- 第1条满足约束条件的路径即为所求







