最小支撑树及图应用

最小支撑树的概念

最小支撑树：包含图G的全部顶点，且包含使子图连通所需的最少的边（n-1）
性质：最小跨边一定在某颗最小生成树里

Prim算法


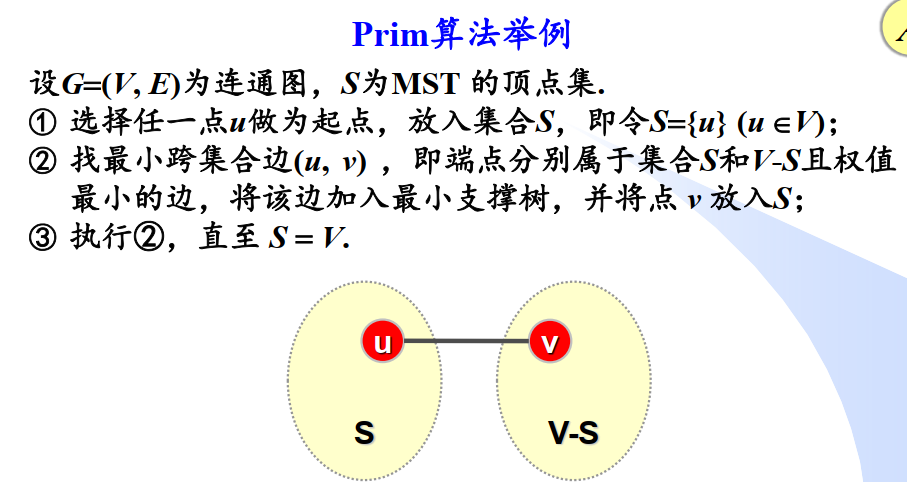
准备工作
Lowcost[v]：顶点v到集合S的最小跨边的权值，初始时Lowcost[u]=0,Lowcost[i]=∞
pre[v]：顶点v到集合S的最小跨边在集合S中的端点，初值-1
S[v]：顶点v是否在集合S中，初值0
时间复杂度O（n^2）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
int FindMin(int S[],int Lowcost[],int n)
{
    int v=-1,min=INF;
    for(int i=1;i<=n;i++)
    {
        if(S[i]==0&&Lowcost[i]<min)
        {
            min=Lowcost[i];
            v=i;
        }
    }
    return v;
}
int Prim(int G[N][N],int n)
{
    int S[N]={0},Lowcost[N],pre[N],ans=0;
    for(int i=1;i<=n;i++)//初始化
    {
        Lowcost[i]=INF;
        pre[i]=-1;
    }
    Lowcost[1]=0;//1作为起点
    for(int i=1;i<=n;i++)//把n个点逐个加入集合
    {
        int v=FindMin(S,Lowcost,n);//找Lowcost最小的点
        if(v==-1) return ans;//不存在跨边，图不连通
        if(v!=1) cout<<pre[v]<<" "<<v;
        ans+=Lostcost[v];
        S[v]=1;//把v加入S
        for(int w=1;w<=n;w++)//更新v的邻接顶点的Lowcost和pre
        {
            if(S[w]==0&&G[v][w]<Lowcost[w])
            {
                Lowcost[w]=G[v][w];
                pre[w]=v;
            }
        }
    }
    return ans;
}

非常类似Dijkstra

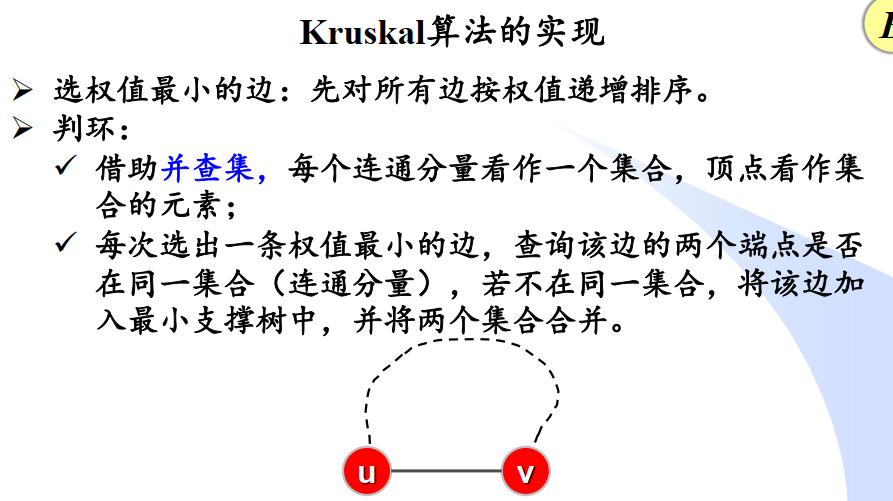
Kruskal算法(逐边加入)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
struct Edge
{
    int head;
    int tail;
    int weight;
};
int Kruskal(Edge* E[],int n,int e)
//E为图的边集数组，n为顶点数，e为边数
{
    for(int i=1;i<=n;i++)//初始化
        Make_set(i);
    Sort(E,e);//对边按权值递增排序
    int ans=0,k=0;//ans为mst边权和,k为已找到的mst边的条数
    for(int i=0;i<e;i++)//从小到大依次扫描每条边
    {
        int u=E[i].head,v=E[i].tail,w=E[i].weight;
        if(Find(u)!=Find(v))
        {
            printf("%d->%d",u,v);
            k++;ans+=w;
            Union(u,v);
        }
        if(k==n-1) return ans;//成功找到mst的全部n-1条边
    }
    return INF;
}

拓展问题

求图的必须包含某些边的最小支撑树->将边的权值置0
最大支撑树 1.边权值取反，求最小支撑树 2.修改Kruskal算法，每次选权值最大的边
最小乘积支撑树:取log

强连通分量

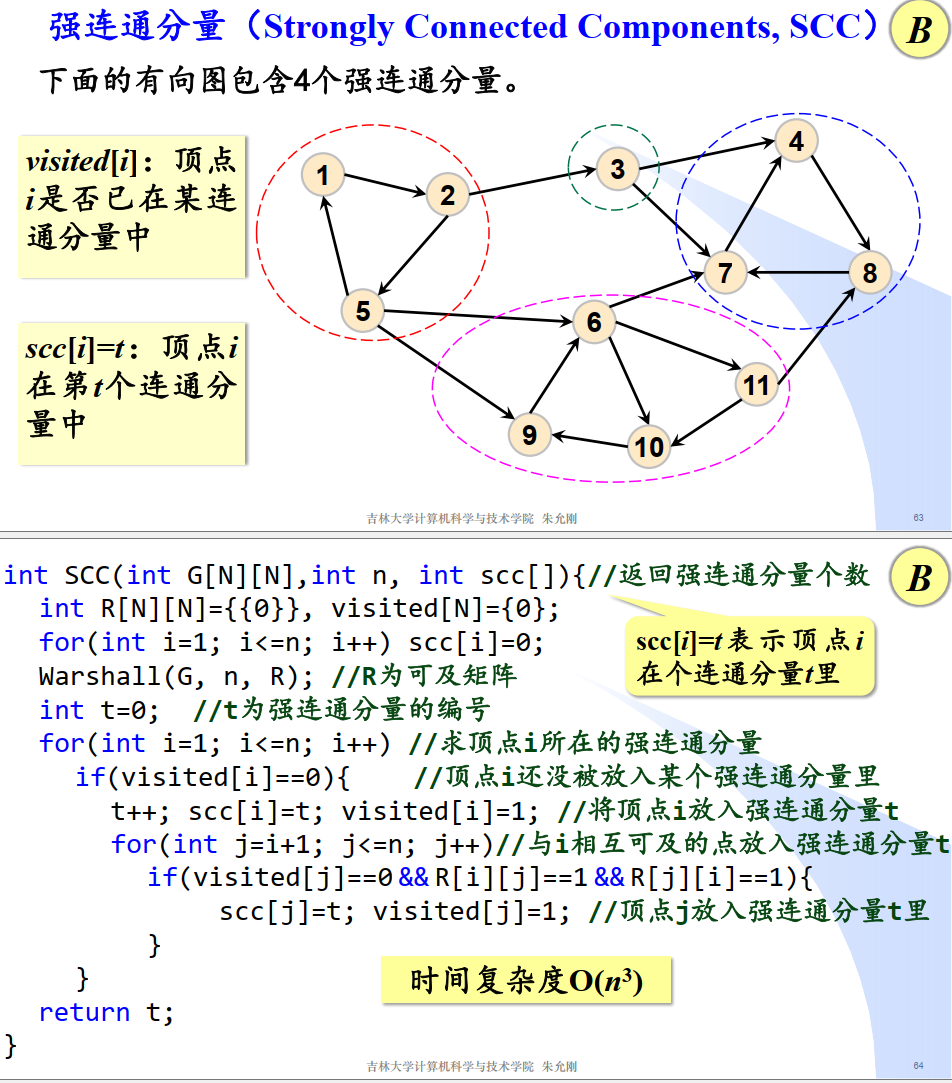
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
int SCC(int G[N][N],int n,int scc[])
{
    int R[N][N]={{0}}, visited[N]={0};
    for(int i=1;i<=n;i++) scc[i]=0;
    Warshall(G,n,R);//R为可及矩阵
    int t=0;//t为强连通分量的编号
    for(int i=1;i<=n;i++)//求顶点i所在的强连通分量
    {
        if(visited[i]==0)
        {
            t++;
            scc[i]=t;
            visited[i]=1;
        }
        for(int j=i+1;j<=n;j++)//将与i相互可及的点放入强连通分量t
        {
            if(visited[j]==0&&R[i][j]==1&&R[j][i]==1)
            {
                scc[j]=t;
                visited[j]=1;
            }
        }
    }
    return t;
}