堆排序

动机
直接选择排序低效原因：每次找最大元素需花费O(n)时间，涉及大量重复比较
能否借助树形结构，减少元素的重复比较次数

锦标赛排序

利用胜者树保存了前面比较的结果，下一次选取最大元素时直接利用前面比较的结果，从而大幅减少关键词比较次数

堆的概念及基本操作

最大堆（大根堆）：一颗完全二叉树，其中任意结点的关键词大于等于它的两个孩子的关键词
最小堆（小根堆）：一颗完全二叉树，其中任意结点的关键词小于等于它的两个孩子的关键词

回顾:完全二叉树的顺序存储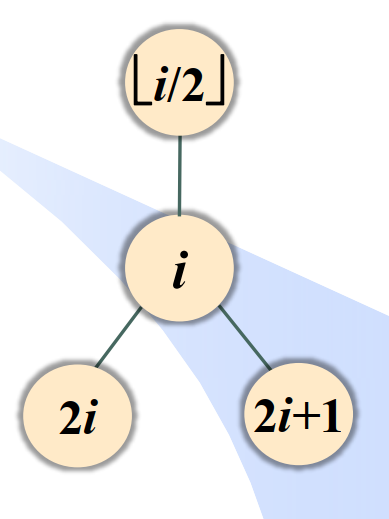

故顺序存储

堆的两个基本操作

上浮操作

当大根堆的元素值R[i]变大时，该结点可能会上浮

1
2
3
4
5
6
7
8
void ShiftUp(int R[],int n,int i)
{
    while(i>1 && R[i]>R[n/2])
    {
        swap(R[i],R[i/2]);
        i/=2;
    }
}

下沉操作

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
当大根堆的元素值R[i]变小时，该结点可能会下沉
```c
void ShiftDowb(int R[],int n,int i)
{
    int maxchd;
    while(i<=n)//i最多下行到最后一个非叶节点
    {
        if((2*i+1<=n)&&(R[2*i]<R[2*i+1]))
            maxchd=2*i+1;
        else
            maxchd=2*i;
        if(R[i]>R[maxchd]) return;
        swap(R[i],R[maxchd]);
        i=maxchd;
    }
}

初始建堆

自顶向下

  • 建立T的左子堆
  • 建立T的右子堆
  • 结点T下沉

自底向上

  • 从最后一个非叶节点开始，依次建立以每个非叶节点为根的子堆
1
2
3
4
5
void BuildHeap(int R[],int n)
{
    for(int i=n/2;i>=1;i--)
        ShiftDown(R,n,i);
}

初始建堆算法的时间复杂度：取决于各结点高度之和
各节点高度之和小于n，算法最坏情况时间复杂度O(n)

堆排序算法

  1. 建堆
  2. for(int i=n;i>1;i–)
    {
    R[1]<->R[i];
    下沉R[1]使R[1]…R[i-1]重新建堆
    }
    时间复杂度O(nlogn)
    不稳定
    1
    2
    3
    4
    5
    6
    7
    8
    9
    void HeapSort(int R[],int n)
    {
        BuildHeap(R,n);
        for(int i=n;i>1;i--)
        {
            swap(R[1],R[i]);
            ShiftDown(R,i-1,1);
        }
    }