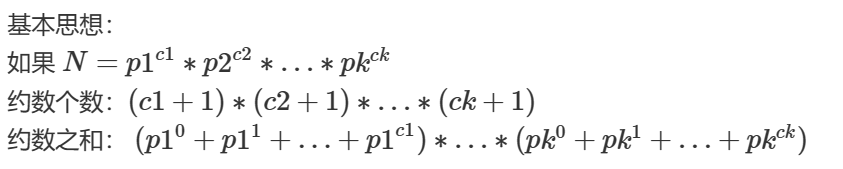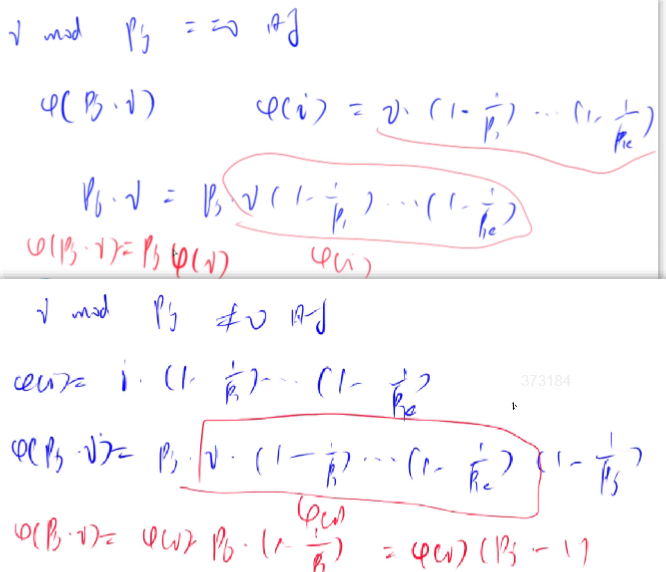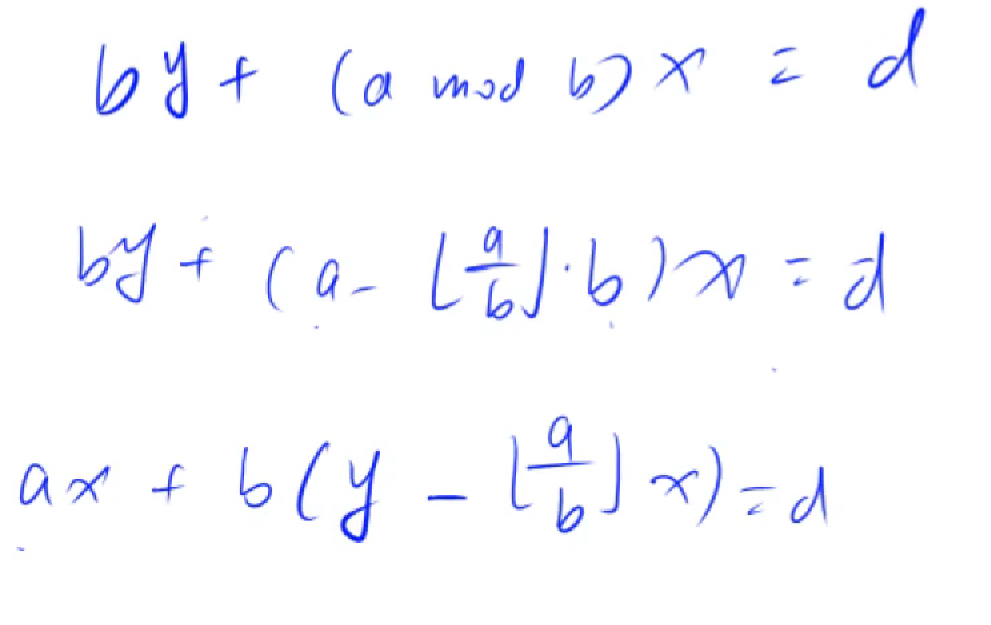数论

质数

判断质数–试除法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
#include <iostream>
using namespace std;

bool is_prime(int x)
{
    if(x<2) return false;
    for(int i=2;i<=x/i;i++)//不建议i*i<=n||i<=sqrt(n)
        if(x%i==0)
            return false;
    return true;
}
int main()
{
    int n;
    cin>>n;
    for(int i=0;i<n;i++)
    {
        int a;
        cin>>a;
        if(is_prime(a)) puts("Yes");
        else puts("No");
    }
}

分解质因数–试除法

性质：n中最多只包含一个大于根号n的质因子

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
#include <iostream>
using namespace std;

void divide(int x)
{
    for(int i=2;i<=x/i;i++)//由于性质，只需要枚举到sqrt(n)
    {
        if(x%i==0)
        {
            int s=0;
            while(x%i==0)
            {
                x/=i;
                s++;
            }
            cout<<i<<" "<<s<<endl;
        }
    }
    if(x>1)//看有没有大于sqrt(n)的质因子
    cout<<x<<" 1"<<endl;
}
int main()
{
    int n;
    cin>>n;
    for(int i=0;i<n;i++)
    {
        int a;
        cin>>a;
        divide(a);
        cout<<endl;
    }
}

筛法

埃氏筛法 O(nloglogn)

不用把每一个数的倍数全部筛掉，只需要把质数的倍数全部筛掉

1
2
3
4
5
6
7
8
void get_primes(int n){
	for(int i=2;i<=n;++i)
		if(!st[i]){
			primes[cnt++]=i;
			for(int j=i+i;j<=n;j+=i) st[j]=true;
		}
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
#include <iostream>
using namespace std;
const int N=1e6+10;
int st[N];
int res=0;
void get_primes(int n)
{
    for(int i=2;i<=n;i++)
    {
        if(!st[i])
        {
            res++;
            for(int j=i;j<=n;j+=i)
                st[j]=1;
        }
    }
}
int main()
{
    int n;
    cin>>n;
    get_primes(n);
    cout<<res;
}

线性筛法 O(n)

线性筛法的核心思路：每一个数n，只会被它的最小质因子筛掉

1
2
3
4
5
6
7
8
9
10
void get_primes(){
    for(int i=2;i<=n;i++){
        if(!st[i]) primes[cnt++]=i;
        for(int j=0;primes[j]<=n/i;j++){//primes[j]<=n/i:变形一下得到——primes[j]*i<=n,把大于n的合数都筛了就没啥意义了
            st[primes[j]*i]=true;//用最小质因子去筛合数
            if(i%primes[j]==0) break;
        }
    }

}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
#include <iostream>
using namespace std;

const int N=1e6+10;
int st[N],primes[N];
int cnt=0;
void get_primes(int n)
{
    for(int i=2;i<=n;i++)
    {
        if(!st[i]) primes[cnt++]=i;
        for(int j=0;primes[j]<=n/i;j++)
        {
            st[primes[j]*i]=1;
            if(i%primes[j]==0) break;
        }
    }
}

int main()
{
    int n;
    cin>>n;
    get_primes(n);
    cout<<cnt;
}

约数

求约数 –试除法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

void get_divisors(int n)
{
    vector<int>ans;
    for(int i=1;i<=n/i;i++)//如果有因数i，必定会有因数n/i
    {
        if(n%i==0)
        {
            ans.push_back(i);
            if(i!=n/i)//避免放入两次
                ans.push_back(n/i);
        }
    }
    sort(ans.begin(),ans.end());
    for(int i=0;i<ans.size();i++)
        cout<<ans[i]<<" ";
    puts("");
}
int main()
{
    int n;
    cin>>n;
    for(int i=0;i<n;i++)
    {
        int a;
        cin>>a;
        get_divisors(a);
    }
}

约数个数

基于算术基本定理

  • N = (p1^x1)(p2^x2)(p3^x3)…(pk^xk)
  • 约数个数=(x1+1)(x2+1)(x3+1)…(xk+1)
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    #include <iostream>
    #include <unordered_map>
    using namespace std;
    const int mod=1e9+7;

    int main()
    {
        int n;
        cin>>n;
        unordered_map<int,int>primes;
        while(n--)
        {
            int x;
            cin>>x;
            for(int i=2;i<=x/i;i++)//分解质因数的过程--试除法
            {
                while(x%i==0)
                {
                    primes[i]++;
                    x/=i;
                }
            }
            if(x>1)
            primes[x]++;
        }
        long long res=1;
        for(auto prime:primes)
        {
            res=(res*(prime.second+1))%mod;
        }
        cout<<res;
    }

约数之和

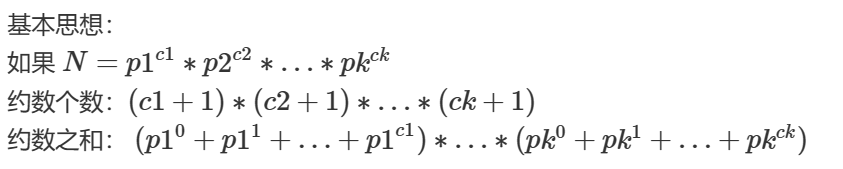
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
#include <iostream>
#include <unordered_map>
using namespace std;
const int mod=1e9+7;
int main()
{
    int n;
    cin>>n;
    unordered_map<int,int>primes;
    while(n--)
    {
        int x;
        cin>>x;
        for(int i=2;i<=x/i;i++)
        {
            while(x%i==0)
            {
                primes[i]++;
                x/=i;
            }
        }
        if(x>1) primes[x]++;
    }
    long long res=1;
    for(auto prime:primes)
    {
        int p=prime.first,a=prime.second;
        long long t=1;
        while(a--) t=(t*p+1)%mod;
        res=res*t%mod;
    }
    cout<<res;
}

欧几里得算法 辗转相除法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
#include <iostream>
using namespace std;
int gcd(int a,int b)
{
    return b?gcd(b,a%b):a;
}
int main()
{
    int n;
    cin>>n;
    while(n--)
    {
        int a,b;
        cin>>a>>b;
        cout<<gcd(a,b)<<endl;
    }
}

欧拉函数

ϕ(n)=n × (p1−1)/p1 × (p2−1)/p2 × … × (pk−1)/pk

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
#include <iostream>
using namespace std;

int main()
{
    int n;
    cin>>n;
    while(n--)
    {
        int x;
        cin>>x;
        int res=x;
        for(int i=2;i<=x/i;i++)
        {
            if(x%i==0)
            {
                res=res/i*(i-1);//把欧拉公式写成这样防止小数出现
                while(x%i==0)  x/=i;
            }
        }
        if(x>1) res=res/x*(x-1);
        cout<<res<<endl;
    }
    
}

筛法求欧拉函数

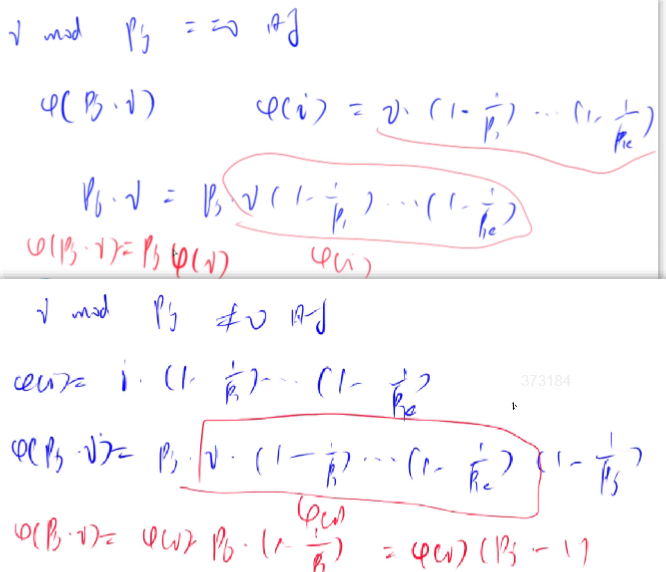
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
#include <iostream>
using namespace std;
const int N=1e6+10;
int st[N],primes[N];
int cnt=0;
int phi[N];

void get_euler(int n)
{
    phi[1]=1;
    for(int i=2;i<=n;i++)
    {
        if(!st[i]) 
        {
            primes[cnt++]=i;
            phi[i]=i-1;
        }
        for(int j=0;primes[j]<=n/i;j++)
        {
            st[primes[j]*i]=1;
            if(i%primes[j]==0) 
            {
                phi[primes[j]*i]=phi[i]*primes[j];
                break;
            }
            phi[primes[j]*i]=phi[i]*(primes[j]-1);
        }
    }
}
int main()
{
    int n;
    cin>>n;
    get_euler(n);
    long long res=0;
    for(int i=1;i<=n;i++)
        res+=phi[i];
    cout<<res<<endl;
}

快速幂

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
#include <iostream>
using namespace std;
typedef long long LL;
int qmi(int a,int k,int p)
{
    int res=1;
    while(k)
    {
        if(k&1) res=(LL)res*a%p;
        k>>=1;
        a=(LL)a*a%p;
    }
    return res;
}
int main()
{
    int n;
    cin>>n;
    while(n--)
    {
        int a,k,p;
        cin>>a>>k>>p;
        cout<<qmi(a,k,p)<<endl;
    }
}
  • 利用快速幂求逆元
    前提：p要是质数
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    #include <iostream>
    using namespace std;
    typedef long long LL;
    int qmi(int a,int k,int p)
    {
        int res=1;
        while(k)
        {
            if(k&1) res=(LL)res*a%p;
            k>>=1;
            a=(LL)a*a%p;
        }
        return res;
    }
    int main()
    {
        int n;
        cin>>n;
        while(n--)
        {
            int a,p;
            cin>>a>>p;
            if(a%p==0) puts("impossible");
            else cout<<qmi(a,p-2,p)<<endl;
        }
    }

扩展欧几里得算法

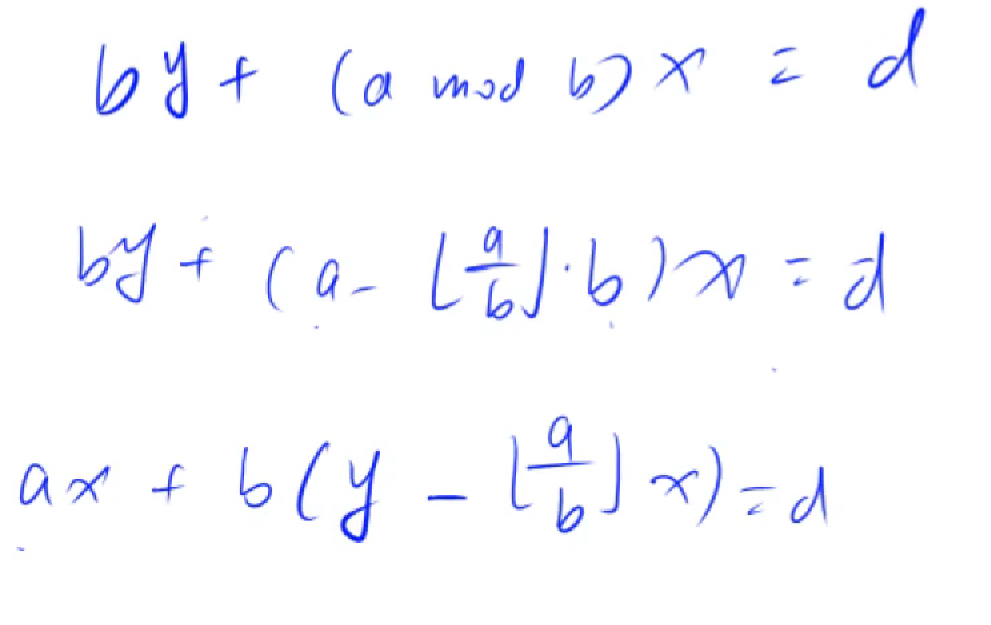
1
2
3
4
5
6
7
8
9
10
int exgcd(int a,int b,int& x,int& y){
    if(b==0){
        x=1; y=0;
        return a;
    }
    int d=exgcd(b,a%b,y,x); // 这里由于 b 的值没有发生变化，但位置作了交换；为了方便讨论，x 和 y 也作交换
    y-=a/b*x;
    return d;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
#include <iostream>
using namespace std;
int exgcd(int a,int b,int&x,int&y)
{
    if(!b)
    {
        x=1,y=0;
        return a;
    }
    int d=exgcd(b,a%b,y,x);
    y-=a/b*x;
    return d;
}
int main()
{
    int n;
    cin>>n;
    while(n--)
    {
        int a,b,x,y;
        scanf("%d%d",&a,&b);
        exgcd(a,b,x,y);
        printf("%d %d\n",x,y);
    }
}

线性同余方程

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
#include <iostream>
using namespace std;

int exgcd(int a,int b,int&x,int&y)
{
    if(!b)
    {
        x=1,y=0;
        return a;
    }
    int d=exgcd(b,a%b,y,x);
    y-=a/b*x;
    return d;
}
int main()
{
    int n;
    cin>>n;
    while(n--)
    {
        int a,b,m;
        scanf("%d%d%d",&a,&b,&m);
        int x,y;
        int d=exgcd(a,m,x,y);
        if(b%d!=0) puts("impossible");
        else printf("%d\n",(long long)x*(b/d)%m);
    }
}