动态规划

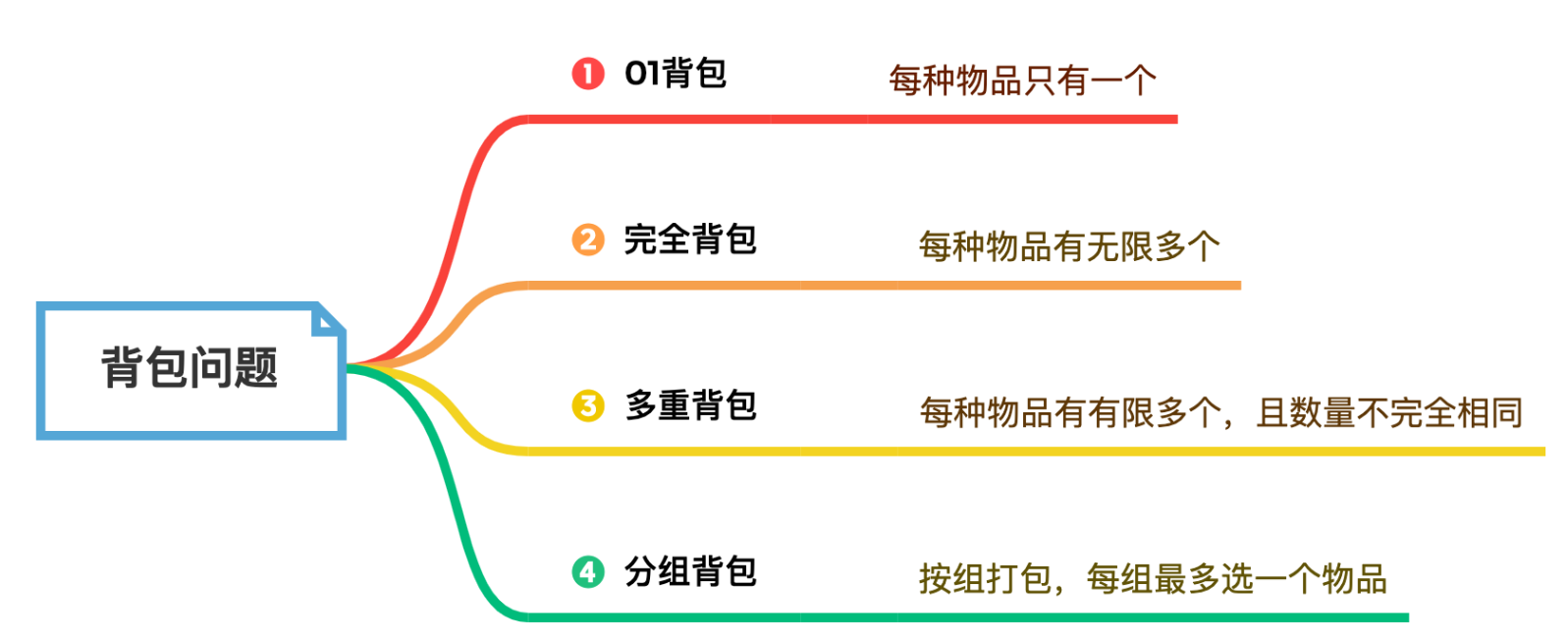
01背包

朴素

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
#include <iostream>
#include <algorithm>
using namespace std;

const int N=1010;
int v[N],w[N];
int f[N][N];
int main()
{
    int n,m;
    cin>>n>>m;
    for(int i=1;i<=n;i++) cin>>v[i]>>w[i];
    for(int i=1;i<=n;i++)
    {
        for(int j=0;j<=m;j++)
        {
            f[i][j]=f[i-1][j];//  当前背包容量装不进第i个物品，则价值等于前i-1个物品 
            if(j-v[i]>=0)
                f[i][j]=max(f[i-1][j],f[i-1][j-v[i]]+w[i]); 
        }
    }
    cout<<f[n][m];
}

滚动数组优化

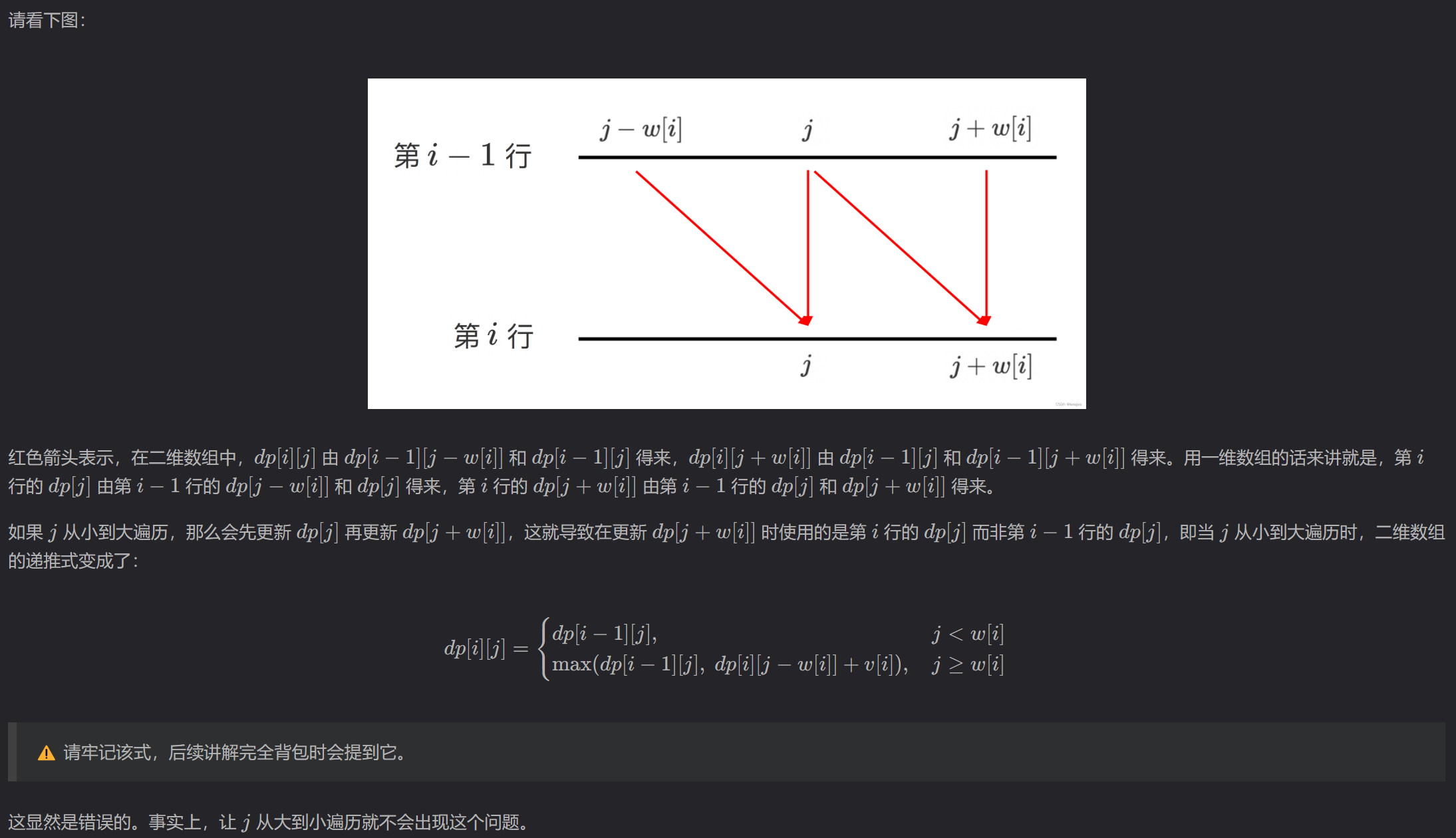
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
#include <iostream>
#include <algorithm>
using namespace std;

const int N=1010;
int v[N],w[N];
int f[N];//删去第一维！
int main()
{
    int n,m;
    cin>>n>>m;
    for(int i=1;i<=n;i++) cin>>v[i]>>w[i];
    for(int i=1;i<=n;i++)
    {
        for(int j=m;j>=v[i];j--)//注意遍历顺序!!!
        {
            f[j]=max(f[j],f[j-v[i]]+w[i]); 
        }
    }
    cout<<f[m];
}

完全背包

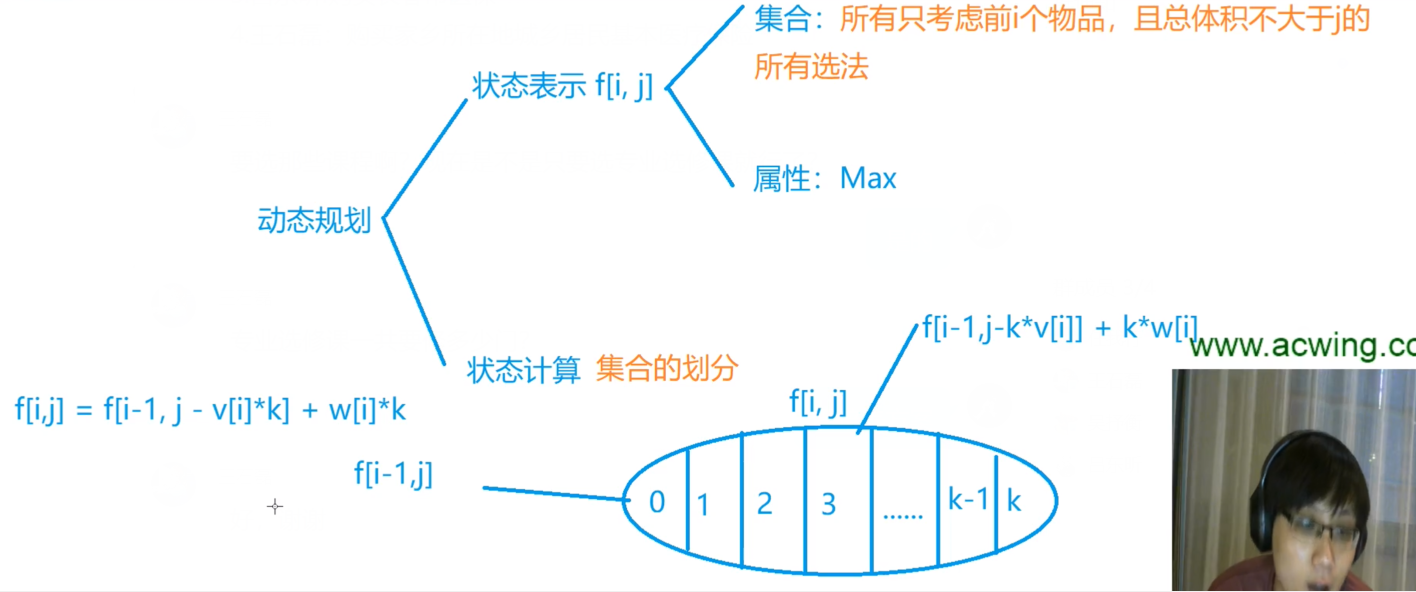
朴素

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
#include <iostream>
#include <algorithm>
using namespace std;
const int N=1010;
int v[N],w[N];
int f[N][N];
int main()
{
    int n,m;
    cin>>n>>m;
    for(int i=1;i<=n;i++) cin>>v[i]>>w[i];
    
    for(int i=1;i<=n;i++)
    {
        for(int j=0;j<=m;j++)
        {
            for(int k=0;k*v[i]<=j;k++)
            {
                f[i][j]=max(f[i][j],f[i-1][j-v[i]*k]+w[i]*k);
            }
        }
    }
    cout<<f[n][m];
}

一重优化

f[i , j ] = max( f[i-1,j] , f[i-1,j-v]+w , f[i-1,j-2v]+2w , f[i-1,j-3v]+3w , …..)
f[i , j-v]= max( f[i-1,j-v] , f[i-1,j-2v] + w , f[i-1,j-3v]+2*w , …..)
由上两式，可得出如下递推关系：
f[i][j]=max(f[i,j-v]+w , f[i-1][j])

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
#include <iostream>
#include <algorithm>
using namespace std;

const int N=1010;
int v[N],w[N];
int f[N][N];

int main()
{
    int n,m;
    cin>>n>>m;
    for(int i=1;i<=n;i++) cin>>v[i]>>w[i];
    
    for(int i=1;i<=n;i++)
    {
        for(int j=0;j<=m;j++)
        {
            f[i][j]=f[i-1][j];
            if(j>=v[i])
            f[i][j]=max(f[i][j],f[i][j-v[i]]+w[i]);
        }
    }
    cout<<f[n][m];
}

滚动数组优化

在一重优化的基础上，利用滚动数组进行二重优化

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
#include <iostream>
#include <algorithm>
using namespace std;

const int N=1010;
int v[N],w[N];
int f[N];

int main()
{
    int n,m;
    cin>>n>>m;
    for(int i=1;i<=n;i++) cin>>v[i]>>w[i];
    
    for(int i=1;i<=n;i++)
    {
        for(int j=v[i];j<=m;j++)//注意与01背包区别！！！
        {
            f[j]=max(f[j],f[j-v[i]]+w[i]);
        }
    }
    cout<<f[m];
}

多重背包

朴素

类似完全背包的朴素做法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
#include <iostream>
using namespace std;
const int N=110;
int v[N],w[N],s[N];
int f[N][N];
int main()
{
    int n,m;
    cin>>n>>m;
    for(int i=1;i<=n;i++) cin>>v[i]>>w[i]>>s[i];
    
    for(int i=1;i<=n;i++)
    {
        for(int j=0;j<=m;j++)
        {
            for(int k=0;k*v[i]<=j&&k<=s[i];k++)//唯一区别！！！
            {
                f[i][j]=max(f[i][j],f[i-1][j-k*v[i]]+k*w[i]);
            }
        }
    }
    cout<<f[n][m];
}

使用二进制优化

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
#include <iostream>
using namespace std;
const int N=12010;//N=nlogs，二进制拆分后的n
const int M=2010;
int v[N],w[N];
int f[M];
int main()
{
    int n,m;
    cin>>n>>m;
    
    int cnt=0;//组号
    for(int i=1;i<=n;i++)
    {
        int a,b,s;
        cin>>a>>b>>s;
        int k=1;//组中元素个数
        while(k<=s)
        {
            cnt++;
            v[cnt]=a*k;
            w[cnt]=b*k;
            s-=k;
            k*=2;
        }
        if(s>0)
        {
            cnt++;
            v[cnt]=a*s;
            w[cnt]=b*s;
        }
    }
    n=cnt;
    
    //转化为01背包问题
    for(int i=1;i<=n;i++)
    {
        for(int j=m;j>=v[i];j--)
        {
            f[j]=max(f[j],f[j-v[i]]+w[i]);
        }
    }
    cout<<f[m];
}

分组背包

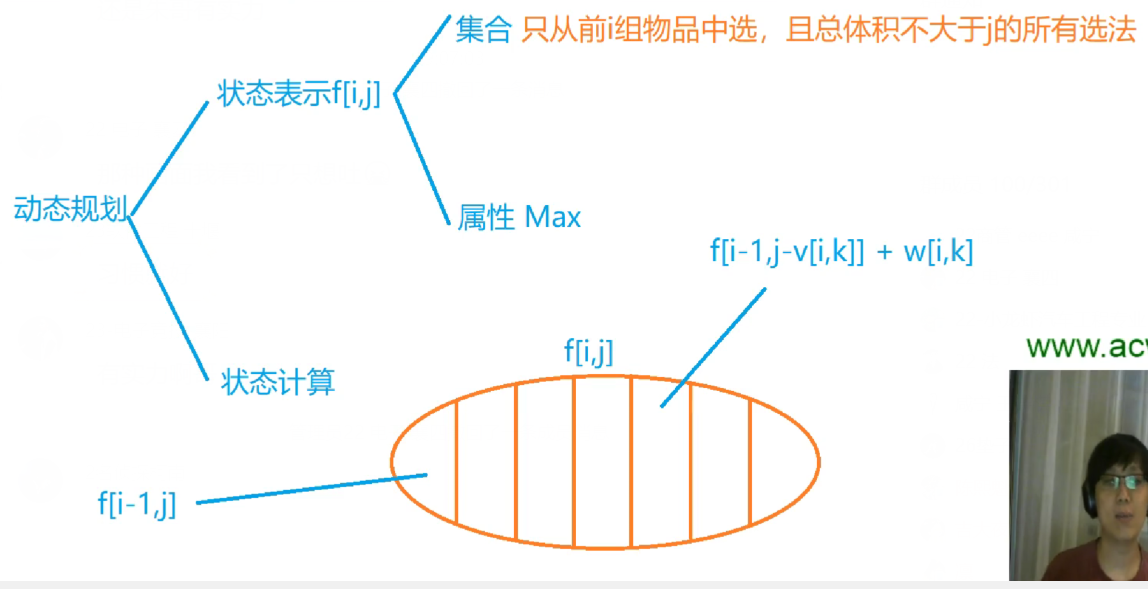
朴素

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
#include <iostream>
using namespace std;
const int N=110;
int v[N][N],w[N][N],s[N];
int f[N][N];

int main()
{
    int n,m;
    cin>>n>>m;
    
    for(int i=1;i<=n;i++)
    {
        cin>>s[i];
        for(int j=1;j<=s[i];j++)
        {
            cin>>v[i][j]>>w[i][j];
        }
    }
    
    for(int i=1;i<=n;i++)
    {
        for(int j=0;j<=m;j++)
        {
            f[i][j]=f[i-1][j];
            for(int k=1;k<=s[i];k++)
            {
                if(j>=v[i][k])
                f[i][j]=max(f[i][j],f[i-1][j-v[i][k]]+w[i][k]);
            }
        }
    }
    cout<<f[n][m];
}

滚动数组优化

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
#include <iostream>
using namespace std;
const int N=110;
int v[N][N],w[N][N],s[N];
int f[N];

int main()
{
    int n,m;
    cin>>n>>m;
    
    for(int i=1;i<=n;i++)
    {
        cin>>s[i];
        for(int j=1;j<=s[i];j++)
        {
            cin>>v[i][j]>>w[i][j];
        }
    }
    
    for(int i=1;i<=n;i++)
    {
        for(int j=m;j>=0;j--)
        {
            for(int k=1;k<=s[i];k++)
            {
                if(j>=v[i][k])
                    f[j]=max(f[j],f[j-v[i][k]]+w[i][k]);
            }
        }
    }
    cout<<f[m];
}