线性DP

数字三角形

c++
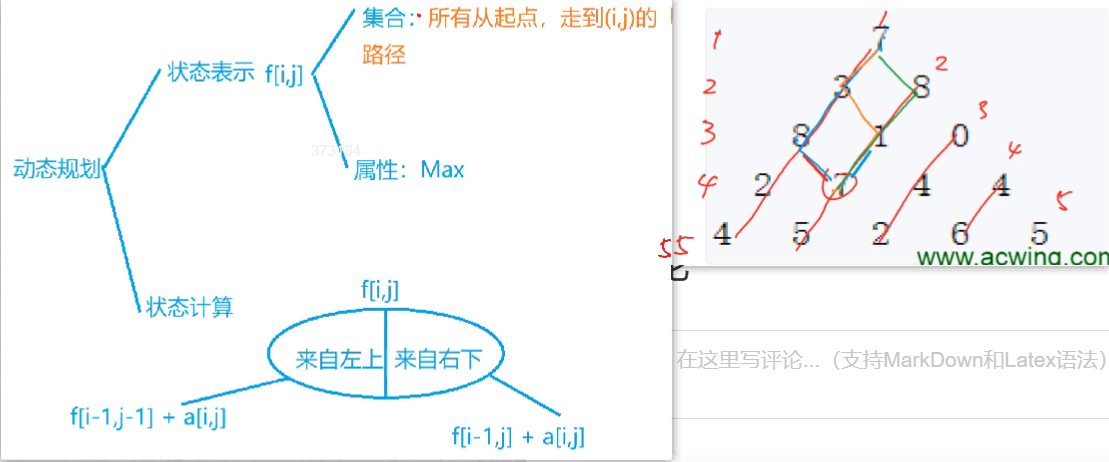
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
#include <iostream>
#include <cstring>
using namespace std;
const int N=510;
const int INF=1e9;
int a[N][N],f[N][N];

int main()
{
    int n;
    cin>>n;
    for(int i=1;i<=n;i++)
        for(int j=1;j<=i;j++)
            cin>>a[i][j];
            
    for(int i=0;i<=n;i++)//初始化
        for(int j=0;j<=i+1;j++)//注意初始化到i+1！！！
            f[i][j]=-INF;
    
    f[1][1]=a[1][1];
    for(int i=2;i<=n;i++)
        for(int j=1;j<=i;j++)
            f[i][j]=max(f[i-1][j-1]+a[i][j],f[i-1][j]+a[i][j]);
    
    int maxn=-INF;
    for(int i=1;i<=n;i++)
        if(f[n][i]>maxn)
            maxn=f[n][i];
    cout<<maxn;
    
}

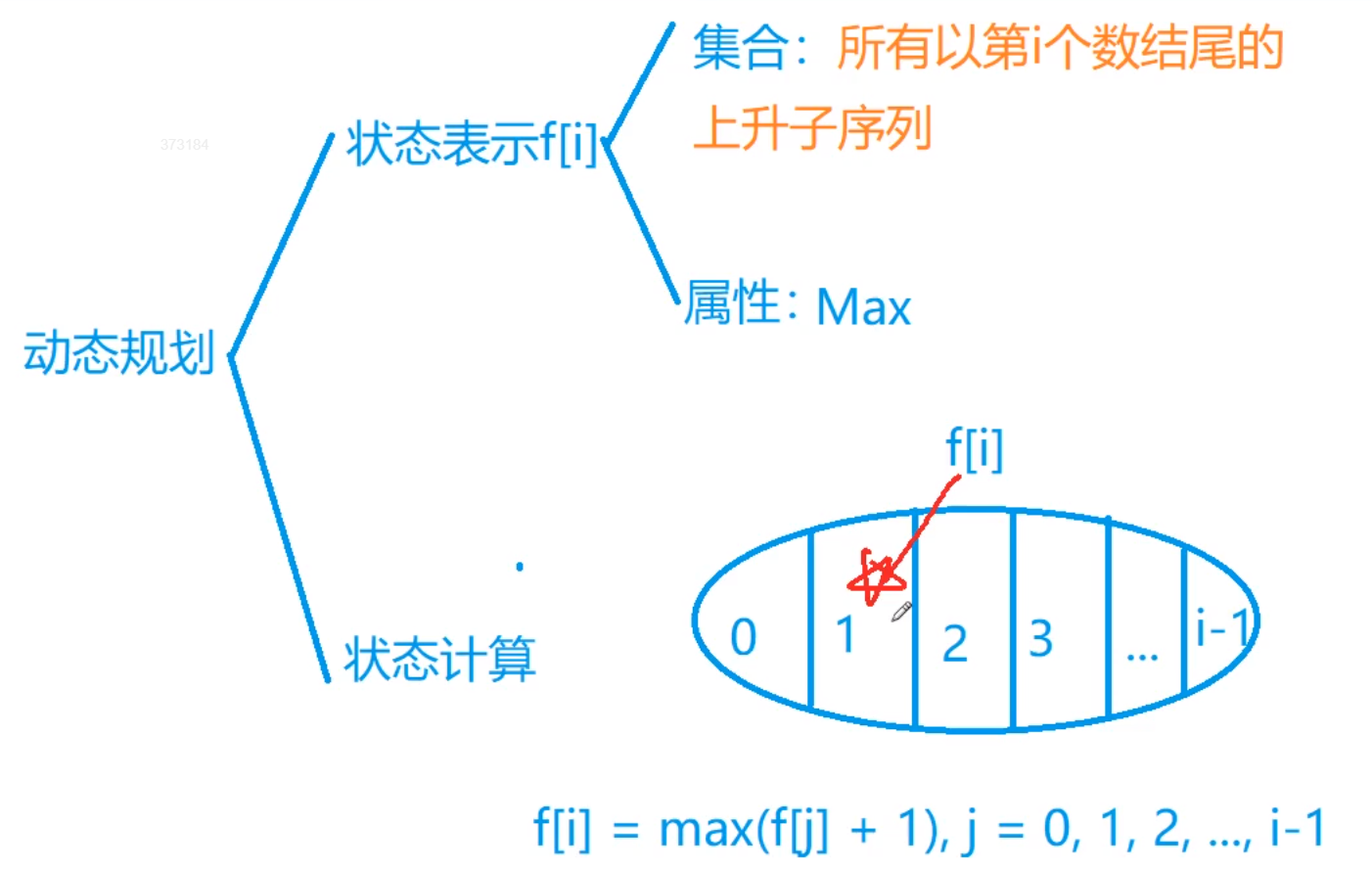
最长上升子序列

概念：所谓最长上升子序列，就是给定一列数，求序列中严格上升（后一个数 > 前一个数）的子序列，这个子序列中数的位置不一定连续

朴素 O(n*n)

c++
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
#include <iostream>
using namespace std;
const int N=1010;
int a[N],f[N];
int main()
{
    int n;
    cin>>n;
    for(int i=1;i<=n;i++) cin>>a[i];
    
    f[1]=1;
    for(int i=1;i<=n;i++)
    {
        f[i]=1;// 设f[i]默认为1，找不到前面数字小于自己的时候就为1
        for(int k=1;k<i;k++)
            if(a[i]>a[k])
                f[i]=max(f[i],f[k]+1);
    }
    
    int maxn=0;
    for(int i=1;i<=n;i++)
        if(f[i]>maxn)
            maxn=f[i];
    
    cout<<maxn;
}

优化 O(nlogn)

c++
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
const int N=100010;
int a[N];
vector<int>stk;
int main()
{
    int n; cin>>n;
    for(int i=1;i<=n;i++) cin>>a[i];
    
    stk.push_back(a[1]);
    for(int i=2;i<=n;i++)
    {
        if(a[i]>stk.back())//如果该元素大于栈顶元素,将该元素入栈
            stk.push_back(a[i]);
        else
        {
            //如果该元素大于栈顶元素,将该元素入栈
            *lower_bound(stk.begin(),stk.end(),a[i])=a[i];
        }
    }
    cout<<stk.size();
}
/*
例 n: 7
arr : 3 1 2 1 8 5 6

stk : 3

1 比 3 小
stk : 1

2 比 1 大
stk : 1 2

1 比 2 小
stk : 1 2

8 比 2 大
stk : 1 2 8

5 比 8 小
stk : 1 2 5

6 比 5 大
stk : 1 2 5 6

stk 的长度就是最长递增子序列的长度

*/

最长公共子序列

c++
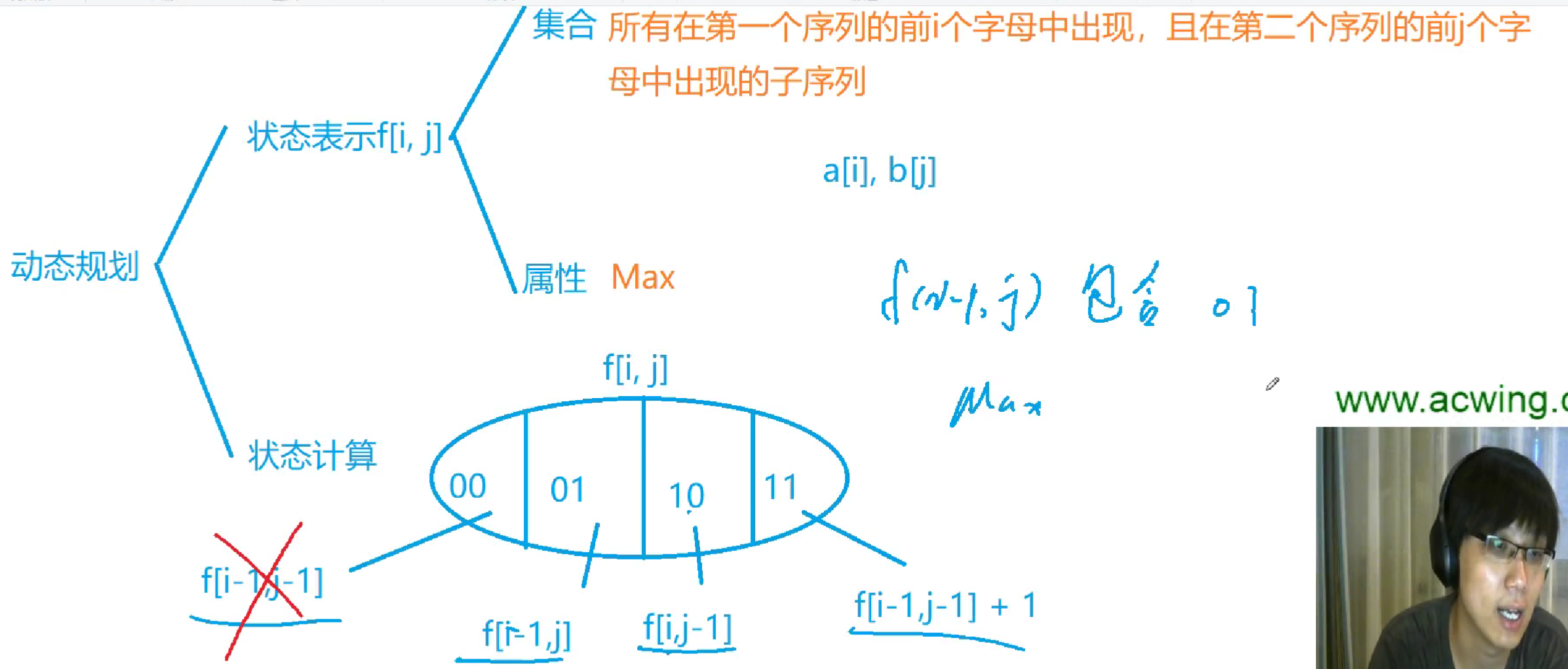
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
#include <iostream>
using namespace std;
const int N=1010;
char a[N],b[N];
int f[N][N];

int main()
{
    int n,m;
    cin>>n>>m;
    cin>>a+1>>b+1;
    
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=m;j++)
        {
            f[i][j]=max(f[i-1][j],f[i][j-1]);
            if(a[i]==b[j]) f[i][j]=max(f[i][j],f[i-1][j-1]+1);
        }
    }
    cout<<f[n][m];
}